Оценка информационного объема и риска модели измерения

Определение количества информационных переменных ММИ. Пропускная способность П статистического эксперимента, полученная в соответствии с его теоретико-информационной моделью [3], позволяет определить количество информационных переменных ММИ, необходимых для получения достаточной входной информации. Для этого определим объём передачи информации модели как разность между энтропией входов (априорной неопределенностью) и средней условной энтропией входов на выходе (апостериорная неопределенность), причем в общем случае каждый из входных параметров характеризуется вероятностью его появления на i -м входе P_i:

П(P_i, f ₁,..., f_n) = H (y) – H (y | x),

где априорная неопределенность H (y) и апостериорная неопределенность H (y | x) определяются следующими выражениями:

H (y)=– P (H ₁)log P (H ₁)–....– P (H_n)log P (H_n)= – P ₁log p ₁–...– P_n log p_n, (2.16)

H (y | x)=–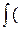 P (H ₁| x)log P (H ₁| x)+ P (H_n | x)log(H_n | x)) f (x) d l(x), (2.17)

в которых f (x) = P ₁ f ₁(x) + P ₂ f ₂(x) +...+ P_nf_n (x). Мера связи между входными и выходными переменными, используя последние выражения для (2.16) и (2.17), определяется в виде

П(P_i; f_i) = 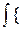P ₁ f ₁(x)log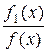+... + P_nf_n (x)log} d l(x) ³ 0,

где P (H, x) d l(x) = P (H | x) f (x) d l(x) – совместная вероятность H и x. Отметим, что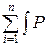 _i (H, x)log 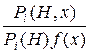d l(x) может быть определена как средняя информация в X относительно H.

Исследуем выражения для априорной информации в виде пропускной способности модели. Пусть f_i (x), i = 1, 2,..., n – плотности распределений, принадлежащих однородному семейству вероятностных мер, а P_i, i = 1, 2,..., n, таковы, что

P ₁ + P ₂ +...+ P_n = 1. (2.18)

Теорема 2.5.1. Максимум величины

П(P_i; f_i) =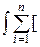 P_if_i (x)log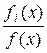] d l(x)

по всевозможным наборам P_i достигается для таких P_i, что

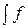₁(x)log 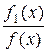d l(x) =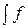₂(x)log 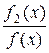d l(x)=...= 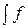_n (x)log] d l(x) (2.19)

и 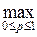П(P_i, f_i) = n равен этой общей величине.

Доказательство. Взяв производную от d П(P_i; f_i)/ dP_i (учтя выражение (2.18)) и приравняв ее к нулю получаем, что

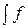_j (x)log 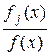d l = _if_i (x)[log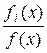]¢ d l. =

= _if_i (x) f_i (x) 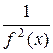f_j (x) d l. = 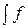_j (x) d l = 1.

Из данного выражения и следует условие (2.19). Из данной теоремы вытекает следствие, которое связывает структуру ММИ и пропускную способность эксперимента, соответствующего ММИ.

Следствие 2.5.1. Многопараметрическая модель измерения, включающая n признаков с плотностями распределения f ₁(x),..., f_n (x), i = 1, 2,..., n, характеризуется максимальной пропускной способностью при условии равенства расхождений между моделью и каждым её признаков.

Определение риска синтеза многопараметрической линейной ММИ. Пусть в общем случае f_i (x_i), i = 1, 2,..., n – плотности распределения признаков x_i ММИ, а f (x ₁, х ₂,..., х_n) – плотность распределения, порожденная линейной ММИ

y = a ₁ x ₁ + a ₂ х ₂ +...+ a_nх_n + a ₀,

причем p (x ₁, х ₂,..., х_n) есть плотность распределения, порожденная истинной ММИ, принадлежащая к тому же семейству вероятностных мер [84]. При этом ММИ определяет теорема эмерджентности, доказательство которой приведено в [3].

Теорема (эмерджентности) 2.5.2. Для различения истинной модели измерения, заданной посредством плотности распределения p (x ₁, х ₂,..., х_n), линейная модель, которая состоит из n признаков с плотностями распределения f ₁(x ₁),..., f_n (x_n), данная посредством плотности распределения f (x ₁, х ₂,..., х_n), содержит информацию меньшую или равную сумме информации, доставляемой признаками модели, т.е.

f_i (x_i)log f_i (x_i)/ p (x ₁, х ₂,..., х_n)] d l(x_i) ³

³ f (x ₁, х ₂,..., х_n)log f (x ₁, х ₂,..., х_n)/ p (x ₁, х ₂,..., х_n)] d l(x ₁, х ₂,..., х_n)

с равенством при условии .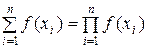

Поскольку многопараметрическая ММИ, удовлетворяющая данной теореме, обладает максимальной пропускной способностью, то она характеризуется минимальным риском для линейной модели. В связи с этим, воспользовавшись введенным в разд. 2.1 понятием риска ММИ параметра и используя свойство аддитивности функционала риска, можно сформулировать следствие.

Следствие 2.5.2. Минимальный риск R _ЛМ многопараметрической линейной ММИ для признаков с интенсивностью риска каждой компоненты модели m _i характеризуется интенсивностью риска:

.

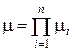Риск многопараметрической линейной модели измерения задается предельным значением риска выбора модели измерения параметра, которое получено в разд. 1.5 и определяется интегральными вероятностными параметрами.

Дата добавления: 2014-01-05