Типовые задачи и примеры их решения. Задача 2.1. Определить риск замены случайной величины х случайной величиной y (согласно выражения 1.1)

Задача 2.1. Определить риск замены случайной величины х случайной величиной y (согласно выражения 1.1), выборочным пространством À для которых является евклидовое пространство R ² двух измерений с элементами Х = (х, y).

Решение задачи. Для решения задачи примем гипотезу H ₁, по которой x и y – зависимые переменные с совместной плотностью распределения f (x, y), и гипотезу H ₂, по которой x и y – независимые переменные с соответствующими плотностями распределений g (x) и h (y). Тогда значение средней информации в y относительно x можно определить как

I (y: x) = 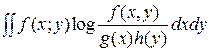. (2.21)

В частности, если H ₁ задает двумерное нормальное распределение с плотностью

f (x, y) = ,

а H ₂ – произведение частных нормальных плотностей распределения

g (x) = 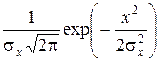h (y) = ,

то находим

R (x, y)=– ==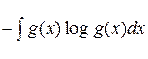

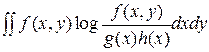= (2.22)

так что R (x, y) является функцией коэффициента корреляции r и изменяется от 0 до ¥, когда 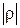изменяется от 0 до 1.

Задача 2.2. Определить приведенный риск передачи сигнала в системе связи на фоне аддитивного шума, обеспечивающий наибольшую информативность (энтропию) при одинаковой мощности излучения.

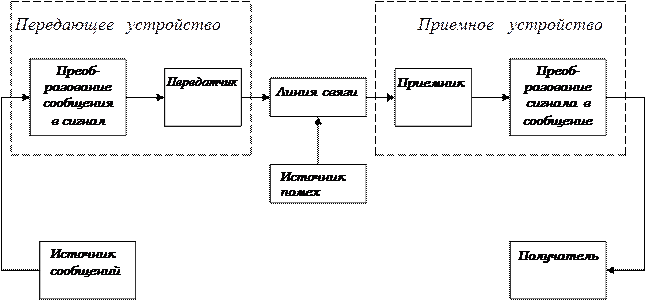
Описание предметной области. Системой связи называется совокупность технических средств для передачи сообщений от источника к потребителю [ Теория передачи сигналов: Учебник для вузов/ А. Г. Зюко, Д. Д. Кловский, М. В. Назаров, Л. М. Финк. – М.: Радио и связь. – 1986. – 304с. ]. Структура данной системы приведена на рис. 2.4. Этими средствами являются передающее устройство, линия связи и приемное устройство.

Основы современной теории связи заложены в важных статьях Найквиста [Nyquist H., “Certain Factors Affecting Telegraph Speed”, Bell System Technical Journal, April 1924, p. 324; “Certain Topics in Telegraph Transmission Theory”, A.I.E.E. Trans., v. 47, April 1928, p. 617.] и Хартли [Hartley R. V. L., “Transmission of Information” Bell System Technical Journal, July 1928, p. 535.]. Основной задачей связи является восстановление (точное или приближенное) в данной точке сигнала, отправленного в другой. Часто сигнал имеет некое значение, то есть соотносится или коррелирует с заданными состояниями некоторой системы. Однако эти семантические аспекты связи не имеют отношения к инженерной задаче, важно лишь то, что сообщение выбирается из некоторого набора возможных. Система связи должна одинаково хорошо работать со всеми возможными вариантами сообщения, а не только с тем, который будет выбран в действительности – на этапе разработки системы это еще неизвестно.

Рис. 2.4. Структурная схема системы связи

Рассмотрим назначение отдельных элементов этой схемы и проиллюстрируем происходящие в них процессы.

Источник сообщения, создающий сообщение или серию сообщений для связи с приемной станцией. Сообщения могут быть различных типов: а) последовательностью букв, как в телеграфной системе; б) некоторой функцией времени f (t), как в системе телефонной связи; в) функцией времени и других переменных, как в телевизионных системах – такое сообщение можно рассматривать как функцию f (x, y, t) двух пространственных координат и времени, представляющую интенсивность излучения в точке (x, y) в момент времени t на фотокатоде; г) двумя или более функциями времени, к примеру f (x), f (y), f(t), как в случае передачи “трехмерного звука” или просто нескольких сигналов одновременно; д) несколькими функциями нескольких переменных – при передаче цветного телевизионного сигнала мы имеем дело с тремя функциями, f (x, y, t), q (x, y, t), h (x, y, t) определенными на трехмерном множестве (можно рассматривать три этих функции также, как компоненты трехмерного векторного поля в пространстве); кроме того, различные виды сигналов могут возникать при передаче телевизионного изображения совместно со звуком каналом.

Передающее устройство, преобразующее неким образом сигнал и делающее его пригодным для передачи по линии связи. В телефонии это сводится главным образом к преобразованию давления звука в пропорциональный электрический сигнал. В случае телеграфа процесс кодирования сигнала преобразует его в последовательность точек, тире и пробелов в линии связи. В многоканальной PCM-системе различные функции различных голосов должны быть дискретизованы, сжаты, закодированы и, наконец, сведены надлежащим образом в один сигнал. Вокодеры (устройства цифрового кодирования речи), телевидение и частотная модуляция – другие примеры сложных преобразований, которым может быть подвергнуто сообщение при формировании сигнала.

Линия связи, представляющая собой среду, используемую для передачи сигнала от передатчика к приемнику. Это может быть парой проводов, коаксиальным кабелем, радиоволнами определенной частоты, лучом света и т.д.

Приемное устройство, выполняющее задачи, противоположные выполняемым передатчиком, а именно – восстановления сообщения из сигнала.

Получатель – человек (или устройство), для которого сообщение предназначено.

В устройстве преобразования сообщения в сигнал непрерывное сообщение, поступающее с выхода источника, преобразуется в форму для передачи. Проходя через линию связи, сигнал подвергается воздействию различного рода помех, и на вход приемника поступает смесь полезного сигнала и помехи. Приемник обрабатывает эту смесь и принимает решение о том, какой сигнал передавался. С выхода приемника сигнал поступает на устройство преобразования сигнала в сообщение и к получателю приходит сообщение, подобное сообщению на выходе источника.

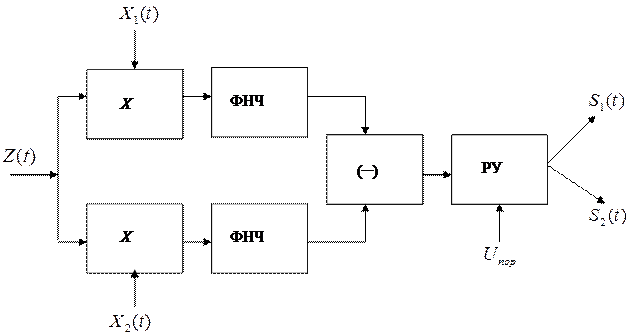
На вход приемника поступает смесь сигнала и помехи Z(t) (рис. 2.5).

Суть когерентного метода приема заключается в том, что на приемной стороне о передаваемом сигнале известно все: частота, фаза, длительность, момент прихода. Поэтому, сигналы Х₁ (t) и Х₂ (t) – точные копии передаваемых сигналов. Устройства умножения эти копии перемножаются с Z (t). Далее произведения Х₁ (t) Z (t) и Х₂(t)Z(t) проходят через ФНЧ, вычитаются в вычитающем устройстве и поступают на вход решающего устройства, где происходит сравнение с пороговым напряжением. Решение принимается в пользу того сигнала, у которого функция взаимной корреляции будет больше.

Ниже рассмотрены некоторые общие задачи, имеющие отношение к системам связи. При этом различные вышеупомянутые элементы представляются математическими величинами, отвлекаясь от их физической сущности.

Рис. 2.5. Структурная схема приемника

Решение. Предположим, что x является переданным сигнальным напряжением, а y – полученным сигнальным напряжением, состоящим из передаваемого сигнального напряжения и аддитивного шума, т.е. y = x + n, где n – шумовое напряжение. Шум и передаваемый сигнал можно считать независимыми, так что

f (x, y) = g (x) h (y | x) = g (x) h (y – x). (2.23)

Риск R (x, y) в соответствии с равенством (2.21) является мерой связи между полученным и переданным сигналами и является в таком случае характеристическим свойством канала связи. В соответствии с экстремальным свойством для нормального закона распределения [96] получаем

f (x, y)=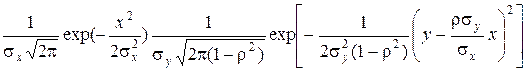,(2.24)

то сравнивая (2.24) и (2.23) видим, что h (y | x) = h (y – x), если

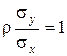, , (2.25)

где S = E (x ²) – средняя мощность передаваемого сигнала, N = E (n ²) – мощность шума. Подставляя величину r² из равенства (2.25) в (2.22) и (2.23), найдем, что потери средней информации в полученном сигнале относительно переданного равны, т.е. приведенный риск

R (x, y) = ,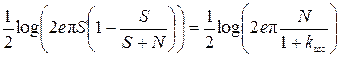

где k _шс = 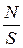– коэффициент шум / сигнал.

Задача 2.3. Определить риск выделения переменных модели измерения, обеспечивающих наибольшую энтропию среди всех распределений с одним и тем же ограниченным интервалом возможных значений непрерывной случайной величины.

Решение. Требование обеспечения наибольшей энтропии при выделении переменных модели измерения определяет то, что при измерении искомые подобласти, формируемые в процессе измерения по искомой модели измерения и соответствующие гипотезам H ₁ и H ₂, характеризуются равномерным законом распределения и в общем случае определяются на интервалах 0 £ x £q₁, 0 £ x £ q₂, q₁ < q₂, причем q₁ < q₂ и

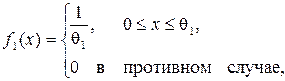
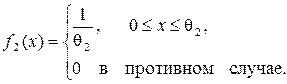
Поскольку для интервала E = { x: q₁ £ x £ q₂} вероятность m₁(E) = 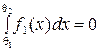, а m₂(E) = 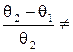0, то m₂ не является абсолютно непрерывной относительно m₁, но мера m₁ абсолютно непрерывна относительно m₂, так как m₁ = 0, когда m₂ = 0. Однако обе меры m₁ и m₂ абсолютно непрерывны относительно меры Лебега. Данное ограничение приводит к тому, что риск формирования достаточной статистики разбиения R (x), определенный в виде функционала расхождения в качестве критерия качества формирования статистики разбиения, вырождается в функционал различия, поскольку изменяется исходное предположение об однородности семейства мер. При этом

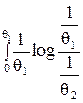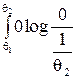R (x) = dx + dx = ,

где f (x) = при 0 £ x £q₁ и f (x) = 0 при q₁ £ x £ q₂, так что, учтя введенное выше смещение, получаем

R (x) = log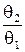= (logq₂ – logq₁) = H_h (q₂) – H_h (q₁), (2.26)

где H_h (q _i) – мера информации по Хартли разбиения соответствующей выборки.

Задача 2.4. Определить риск передачи сигнала на фоне аддитивного шума, относящегося к классу всех положительных непрерывных случайных величин с одним и тем же математическим ожиданием, и имеющего наибольшую энтропию.

Решение. В соответствии с экстремальным свойством экспоненциального закона распределения для решения данной задачи определим риск для экспоненциальной популяции f_i (x) = exp[– (x – q _i)] (q _i £ x £ ¥) и f_i (x)= 0 (– ¥< x < q _i), i = 1, 2, q₁ > q₂. Находим, что

R (y, x) = log e – 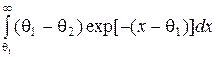= log e – q₁

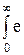xp(– x) x log e dx = log e

и для выборки О_n в n независимых наблюдений R (y, x; О_n)= n R (y, x; О ₁) = n (q₁–q₂). Известно, что если À – пространство выборок в n независимых наблюдений и Y = T (x) = min(x ₁, x ₂, …, x_n), то g_i (y)= n exp[– n (y – q_i)], q _i £ y £ ¥, и нулю в противном случае, i = 1, 2, является достаточной статистикой.

Задача 2.5. Определить риск для пуассоновской популяции.

Решение. Рассмотрим пуассоновские популяции с параметрами l₁, l₂. Находим, что

I (1:2) = ,

и для случайной выборки О_n в n независимых наблюдений

I (1:2; О_n)= n I (1:2; О ₁) = ,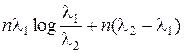

и, следовательно, статистика 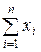является достаточной статистикой для пуассоновских популяций.

Дата добавления: 2014-01-05