Асимптотический метод выделения признаков модели измерения

Выделение общей ММИ сводится к определению каждого из ее признаков, т.е. выделение соответствующего класса, который определяется областью определения этого признака в общей области определения всей модели. Таким образом, задача выделения признака ММИ, постановка которой приведена в разд. 3.3, заключается в разбиении области определения общей ММИ на области определения каждого признака. В частном случае, если область определения двухпризнаковой общей модели (пространство выборок в n независимых наблюдений) X разбита на непересекающиеся множества E и 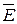(Е Ç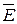= 0, X = E È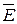) индикатором множества c_E(x). Причем процедура разбиения заключается в том, что если выборка x Î E (c_E(x)=1), принимается гипотеза H ₁ (отвергается H ₂), и если выборка x Î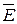(c_E(x)=0), принимается гипотеза H ₂ (отвергается H ₁). Гипотеза H ₂ рассматривается как нулевая гипотеза, а E является критической областью. Вероятность неправильного принятия гипотезы H ₁, ошибка первого рода, равна a= P (x Î E ₁| H ₂)=m₂(E ₁), а вероятность неправильного принятия гипотезы H ₂, ошибка второго рода, равна b = P (x Î E ₂| H ₁) = m₁(E ₂).

При этом риск разбиения, в соответствии с теоремой 3.1 [66], которая определяет условия минимума различающей информации, для статистики Т (x)=c_E(x) определяется выражением

R _р(1:2) ³ (2.20)

с равенством, совпадающим с минимумом, при

f ₁(x) =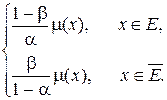

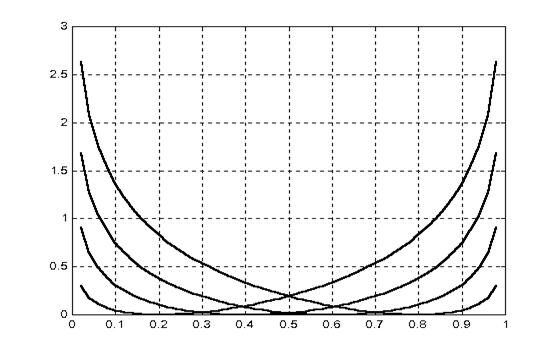
Установленные в данном выражении зависимости риска разбиения от вероятности ошибки первого и второго рода при последовательном накоплении информации измерения приведены на рис. 2.2 и 2.3 соответственно.

Данные выражения позволяют разбивать пространства X с ошибками a, b без потери информации, поскольку это разбиение достаточное. Причем риск выбора модели для соответствующих переменных при заданных значениях ошибок их идентификации a, b по областям определения можно получить, равным нулю (рис. 2.2, 2.3). В общем случае, если E_i Î S, i = 1,2,..., E_i Ç E_j и X = È E_i, т.е. если Х разбито на попарно непересекающиеся множества E ₁, E ₂,..., то в соответствии со следствием 3.3.2 [66]

R _р(1:2) ³ ,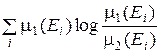

а равенство достигается при условии

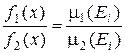
для x Î E_i, i = 1, 2,...

b

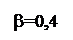
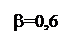
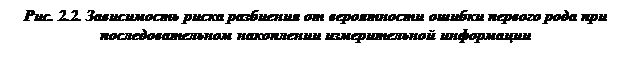
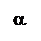
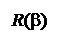
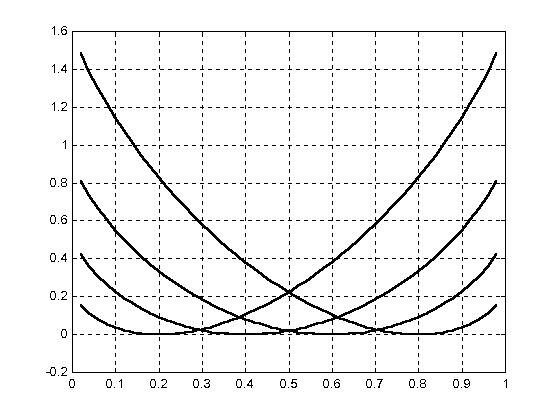
При оценке качества асимптотического выделения признака ММИ методом последовательного анализа, необходимо использовать теорему 4.3.1 [66], которая совпадает с выражением, полученным в разделе 3.8.

Теорема:

R _р(O_n) = nR _р(O ₁) ³ blog+ (1 – b)log,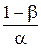

где O_n – выборка в n независимых наблюдений, а O ₁ – выборка, состоящая из одного наблюдения.

Для фиксированного значения a, скажем a₀, 0 < a₀ < 1, нижняя граница минимума всех возможных b = b _n * получается из формулы

R _р(O ₁) ³ n ^–1a₀log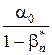+ (1 – a₀)log.

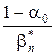Аналогично, для фиксированного значения b₀, 0<b₀<1, нижняя граница a, a _n * получается из формулы

R _р(O ₁) ³ n ^–1b₀log+ (1 – b₀)log.

Величины R _р(1:2; X)/ R _р(1:2; Y) и R _р(2:1; X)/ R _р(2:1; Y) могут быть использованы (для больших выборок) как мера относительной эффективности конкурирующих переменных X и Y в том смысле, что

R _р(1:2; X)/ R _р(1:2; Y) = n_y / n_x или R _р(2:1; X)/ R _р(2:1; Y) = N_y / N_x,

где n_x, n_y и N_x, N_y – соответственно объемы выборок, необходимых для того, чтобы получить для данного b₀ то же a _n * и для данного a₀ – то же b _n *.

Дата добавления: 2014-01-05