Исследование сходимости алгоритма

Исследование условий монотонной сходимости. Для исследования условий сходимости рассматриваемых алгоритмов, обозначим q _xi (N) = x_i – x_i (N), а формулу (3.16) перепишем в более удобном виде

q _xi (N)=q _i (N –1)–g _i [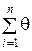 _i (N –1) k_i (N)][ 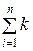_i ²(N)]^–1 x_i (N), (i =1, 2,..., n).(3.19)

Теорема 3.7.1. Необходимым условием монотонной сходимости алгоритма (3.17) является условие линейной независимости всех n составляющих вектора входных воздействий, а все диагональные элементы матрицы Г g _i должны быть равны между собой, то есть

Г = a Е, (3.20)

где E – единичная матрица, причем a – скаляр, принимавший значения из интервала 0<a<2, g _i =a (i = 1, 2,..., n); 0<a<2.

Из данной теоремы, доказательство которой приведено в работе [3], следует, что при оптимальном одношаговом алгоритме оценка i -го параметра, в соответствии с выражением (3.11), уточняется на величину D(N) k _i (N) (g _i D(N) k _i (N)), а критерием исправления оценок служит ошибка предсказания. Если же условия для матрицы Г не выполняется, то алгоритм не обладает монотонной сходимостью, но при этом сохраняется его сходимость по вероятности. Поэтому матрицу Г оптимального одношагового алгоритмаестественно назвать матрицей сходимости.

Причем для обеспечения необходимых условий данной теоремы могут быть использованы результаты преобразования переменных в независимые в разделе 3.6 [3].

Определение скорости сходимости алгоритма. Скорость сходимости алгоритма определяется выбранной оценкой статистики результатов измерения, а также объемом данной статистики. Общий анализ асимптотических свойств квадратичного критерия оценки, проведенный в работе [3], показал, что используемый функционал риска относится к классу критериев согласия интегральных статистик типа Крамера – фон Мизеса – Смирнова w _{n ,1}² (q º1, k =2), локальные точные наклоны с (x) соответствующей оценки 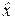для которого равны 2p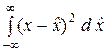[93]. При этом относительная асимптотческая эффективность оценки по Бахадуру е_V,T^B (b, x) для обобщенного варианта статистики w _n,q ², при q (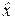) = p (x), определяется отношением рисков оценки соответствующих выборок:

е_V,T^B (b, x)==== ,

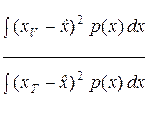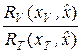где N_T (a, b, x), N_V (a, b, x) – минимальный объем выборки, необходимый для того, чтобы используемый критерий качества оценки 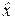уровня a, основанный соответственно на статистике { T_n }, { V_n }, имел в точке x мощность, не меньшую b.

Таким образом, при сравнении двух статистик { V_n } и { T_n } статистика, характеризующаяся большим значением риска оценки, является эффективней, оценка которой быстрее сходится к своему истинному значению. Это позволяет сформулировать адаптивный метод оценивания параметра измерения. В данном методе управляя риском [1], например, путем добавления в оценку смещения, можно увеличить сходимость АОЭИ. После определения оценки по экспериментальным данным можно убрать смещение из полученного результата.

Проведенный в работе [3] анализ используемого адаптивного алгоритма, описанного в разд. 3.4, показал, что при отсутствии погрешности измерения одношаговый алгоритм (3.9) сходится при весьма слабых ограничениях: достаточно, чтобы входные переменные изменялись линейно независимо. Влияние входных переменных на скорость сходимости гораздо сильнее.

Наибольшая скорость сходимости получается, если входные векторы ортогональны в разных тактах, то есть, когда x ^T(j) x (s)= 0, если j ¹ s. Если размерность вектора x равна n, то существует только n линейно независимых векторов, ортогональных друг другу. Используя условие ортогональности и формулу (3.10), получаем после n тактов уточнения (при g = 0):

q ^Т(N) q (N) = q ^Т(0) q (0){1 – S(q ^T(0) k (j))²[(q ^T(0) q (0) k ^T(j) k (j)]^–1}.

Сумма в фигурных скобках – это сумма квадратов направляющих косинусов вектора q (0) и потому равна единице, а выражение в фигурной скобке соответственно нулю. Следовательно, при ортогональных воздействиях на входе после n шагов все коэффициенты будут определены совершенно точно и рассматриваемый алгоритм не хуже по быстродействию любого другого, так как для определения коэффициентов в общем случае требуется n уравнений (испытаний). Выбирать векторы входных воздействий ортогонально друг другу можно только, если они управляемы, поэтому при активном эксперименте входные векторы следует устанавливать ортогонально друг другу.

Скорость сходимости тем меньше, чем меньше отличаются направления векторов в соседних опытах. Если угол между двумя соседними направлениями f, то после N шагов ошибка (с точностью до первого шага) будет равна

q ^T(N) q (N) = q ^T(0) q (0)соs ^N f.

Для многомерного случая данный вывод сохранится, то есть чем ближе к 90⁰ возможный угол между векторами, тем выше скорость сходимости. При измерении это условие обеспечить невозможно, поэтому можно вести речь о статистической ортогональности. Если, к тому же, математические ожидания компонент всех векторов равны нулю и имеют одинаковые дисперсии, то математические ожидания ошибки после N шагов [84] равны

M{ q ^T(N) q (N)} = (1 – n ^–1) ^N q ^T(0) q (0). (3.21)

Независимое изменение компонент вектора x обеспечивает наибольшую скорость сходимости. При этом ошибка уменьшается по экспоненте.

Если математические ожидания входных переменных не равны нулю, то скорость сходимости замедляется, поскольку уменьшается угол возможных направлений для входного вектора, а следовательно, и для вектора уточнения коэффициентов. Если при нулевых математических ожиданиях и независимости входов вектор входов может принимать любые направления в пространстве, то при большом, по сравнению с среднеквадратическим, отклонении математического ожидания вектора входных воздействий движение возможно только в небольшом угле около вектора математического ожидания. Большое математическое ожидание резко уменьшает угол возможных направлений. Отсюда следует, что строить вычислительную модель АОЭИ необходимо относительно математических ожиданий входных переменных или их оценок. Это позволяет не только увеличить скорость сходимости, но и снизить требования к арифметическим устройствам (уменьшить их разрядность).

Аналогичное влияние на скорость сходимости оказывает корреляция входных переменных между собой. Чем сильнее коррелированны входы, тем меньше скорость сходимости. Хотя, при наличии корреляции, вектор входных воздействий может принимать любые направления, на самом деле наиболее вероятными оказываются направления, сосредоточенные в узком секторе.

Дата добавления: 2014-01-05