Выбор критерия близости

Для определения качества процедуры формирования модели измерения, могут быть выбраны критерии близости, использующие разные подходы их формирования.

I. В алгоритмах формирования, использующих детерминированные признаки в качестве меры близости, естественно применить среднеквадратическое расстояние между данным объектом w и совокупностью объектов (w ₁, w ₂,...., w_n), представляющих (описывающих) каждый класс. Для сравнения с классом W_g это выглядит так:

,

где k_g – количество объектов, представляющих W_g -й класс.

При этом в качестве методов измерений расстояния между объектами d (w, w_g) могут использоваться любые методы. Так, если сравнивать непосредственно координаты (признаки), то

,

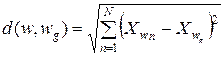где N – размерность признакового пространства.

Если сравнивать угловые отклонения, то рассматривая вектора, составляющими которых являются признаки КО w и класса w_g, будем иметь

,

где 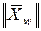| и 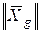– нормы соответствующих векторов.

В алгоритме формирования, использующем детерминированные признаки можно учитывать и их веса V_j (устанавливать степень доверия или важности). Тогда рассмотренное среднеквадратическое расстояние принимает следующий вид:

.

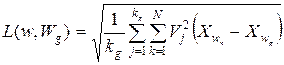II. В алгоритмах формирования, использующих вероятностные признаки, в качестве меры близости используется риск, связанный с решением о принадлежности объекта к классу W_i, где i – номер класса. (i = 1, 2,.., m.).

Пусть описание классов представлено

.

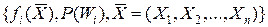В рассматриваемом случае к исходным данным для расчета меры близости относится платежная матрица вида

.

Здесь на главной диагонали – потери при правильных решениях. Обычно принимают С_ii =0 или C_ii <0.

Если вектор признаков контролируемого объекта w – 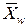, то риск, связанный с принятием решения о принадлежности этого объекта к классу W_g, когда на самом деле он может принадлежать классам W ₁, W ₂,..., W_m, наиболее целесообразно определять как среднее значение потерь

С _{1 g} , C _{2 g} ,..., C_mg,

то есть потерь, стоящих в g -м столбце платежной матрицы. Тогда этот средний риск можно записать как

,

где P (W_i | X_w) – апостериорная вероятность того, что w 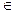W_i.

Для исходных данных, а именно описаний классов, эта вероятность легко может быть определена в соответствии с теоремой гипотез или по формуле Байеса:

.

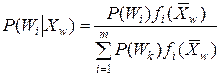III. В наиболее общем случае, когда приходится при формировании модели измерения использовать информацию гетерогенного характера, т.е. разнообразную по характеру и содержанию, необходимо применять информационный критерий близости. При этом статистика, определенная разбиением À = 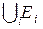, является достаточной для различения, если À разбито на попарно непересекающиеся множества и

I (1:2) = ,

где m₂(E ₁) = P (x Î E ₁| H ₂) – вероятность неправильного принятия гипотезы H ₁ (ошибка первого рода); m₁(E ₂) = P (x Î E ₂| H ₁) – вероятность неправильного принятия гипотезы H ₂ (ошибка второго рода).

Из общего анализа процедуры различения можно сформулировать характерные требования, которым должен удовлетворять критерий, определяющий различения между выборками, полученными в результате измерения. Так, в среднем различающая информация, получаемая из статистических наблюдений, положительна. Все x Î E, для которых выполнено условие равенства, можно рассматривать как эквивалентные в задаче различения. Если распределения, соответствующие обеим гипотезам совпадают, то различающая информация не существует. При этом группировка, сгущение или другие преобразования наблюдений с помощью статистики ведут в общем случае к потере информации. В случае достаточной статистики разбиения, когда самые крупные элементы группировки содержат в себе такую же информацию, как разбиение с элементами в виде точек исходного пространства, информация не теряется. Достаточность статистики для семейства распределений не нарушается при усечении или при отборе в соответствии с функцией j(x) = f(T (x)).

Если разбиение пространства X удовлетворяет необходимому и достаточному условиям, т.е. если плотности распределения x при условии E_i одни и те же для обеих гипотез по всем членам разбиения, то можно определить разбиение X = 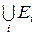как достаточное разбиение для различения. При достаточности разбиение с самыми крупными элементами группировки содержит в себе такую же информацию, как разбиение с элементами в виде точек пространства X. Понимая под статистикой разбиение пространства X на множества эквивалентных x, можно сказать, что статистика, определенная разбиением X = 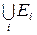является достаточной для различения, если необходимое и достаточное условие того, что информация не уменьшается после группировки 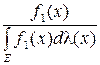=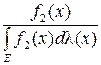выполнено, т.е. “статистика отбирает для суммирования всю относящуюся к делу информацию, доставляемую выборкой” [77].

Пусть Y = T (x) – статистика, т.е. T (x) является функцией с областью определения X и областью значений Y, и пусть Г – аддитивный класс подмножеств Y. Предположим, что T (x) – измеримая функция, т.е. для любого множества G Î Г полный прообраз T ^{– 1}(G)={ x: T (x)Î G } [ T ^{– 1}(G) – есть совокупность элементов x таких, что T (x)Î G ] прнадлежит классу S измеримых подмножеств пространства X. Класс всех множеств вида T ^{– 1}(G), где G ÎГ, обозначается T ^{– 1}(Г). Таким образом, имеем измеримое отображение T вероятностного пространства (X, S, m _i) в вероятностное пространство (Y, Г, v_i), где v_i (G) m _i (T ^{– 1}(G)).

Если определить g(G) = l(T ^{– 1}(G)), v ₁ º v ₂ º g (меры абсолютно непрерывны одна относительно другой), то теорема Радона – Никодима позволяет утверждать существование таких плотностей вероятности g_i (y), i = 1, 2, что

v_i (G) = , i = 1, 2, G Î Г,

для всех G Î Г. Функция g_i (y) является условным математическим f (x) при условии T (x) = y и обозначается E _l(f_i ½ y). В этом случае в терминах вероятностных пространств (Y, G, v_i), i = 1, 2, различающая информация определяется различием

I (1:2; G) =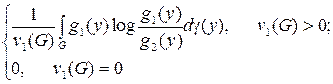

и

I (1:2; Y) = .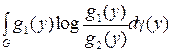

При этом вероятностные меры m₁ и m₂ должны быть абсолютно непрерывны одна относительно другой. Это требование связано с возможностью определения I (1:2) и I (2:1), чтобы могло существовать расхождение

J (1:2) = I (1:2) + I (2:1) = ,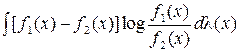

которое и определяет информационное различие между двумя элементами.

IV. Для алгоритмов, основанных на логических признаках, достаточно подставить их в булевы соотношения между классами и признаками, чтобы сразу получить результат как истинность или ложность булевой функции описания того или иного класса.

V. Для алгоритмов, основанных на структурных (лингвистических) признаках, понятие “меры близости” более специфично.

С учетом того, что каждый класс описывается совокупностью предложений, характеризующих структурные особенности объектов соответствующих классов, выбор неизвестного объекта осуществляется идентификацией предложения, описывающего этот объект с одним из предложений в составе описания какого-либо класса. При этом идентификация может подразумевать наибольшее сходство предложения, описывающего контролируемый объект с предложениями из наборов описания каждого класса.

Формирование модели осуществляется последовательными приближениями по мере получения дополнительной информации. В этом ряду последовательных приближений главную роль играют признаки измерения. От эффективности их набора зависит эффективность модели контролируемого объекта в целом. В процессе совершенствования модели указанный набор пополняется, неэффективные признаки исключаются. Поэтому одной из задач формирования модели должна быть и задача перехода от априорного словаря признаков к рабочему. То же касается и априорного алфавита классов.

Дата добавления: 2014-01-05