Взаимосвязь размерности вектора признаков и вероятности правильности формирования модели измерения

Взаимосвязь размерности алфавита классов и качества и эффективности модели измерения

Оптимизация алфавита классов и словаря признаков

Процесс формирования модели включает последовательность операций:

– прием на входе устройства формирования образа модели;

– сопоставление апостериорной информации поступившего контролируемого объекта с имеющимся в устройстве формирования априорным описанием классов всех объектов, подлежащих распознаванию (объектов, на которые рассчитана система);

– принятие решения об отнесении модели, которая была принята, к одному из классов.

Правило, согласно которому модель, образ которой принят, ставится в соответствие наименование класса, называется решающим правилом. Центральной задачей формирования считается нахождение в признаковом пространстве таких границ, которые некоторым оптимальным образом (например, по критерию минимума ошибок выбора) разделяют это пространство на области, соответствующие классам.

В зависимости от объема априорной информации возможно два подхода к определению решающих правил:

1. Непосредственное предварительное определение при достаточном количестве априорной информации (устройство формирования без обучения).

2. Постепенное уточнение в ходе работы устройства формирования по назначению при наборе достаточного количества информации (обучающиеся устройство формирования).

Каждый их подходов основан на том, что априорный словарь признаков и алфавит классов известны. При отсутствии априорного алфавита классов применяется подход, реализуемый в самообучающемся устройстве формирования. Однако при этом заранее должны быть известны словарь признаков и, кроме того, набор некоторых правил назначения классов в процессе самообучения. Решающие правила здесь определяются как итог нахождения алфавита классов.

Для логических устройств формирования решающие правила – это правила определения неизвестных в булевых уравнениях, а в структурных – правила определения правильности конструкции предложения.

При рассмотрении задачи формирования МИ важнейшими этапами являются определение рабочего алфавита классов и рабочего словаря признаков устройства формирования. Однако при окончательном решении эвристической задачи выбора признаков, а также при планировании использования как априорных (описание классов), так и апостериорных данных (измерения по данному неизвестному подлежащему классификации объекту), дополнительную информацию предоставляют взаимосвязи между признаками. Упоминаемые взаимосвязи могут принимать различные формы, иметь свои особенности.

В управлении формированием модели высокие качество и эффективность принятых решений достигается:

1. Увеличением числа классов в принятом алфавите, то есть, повышением степени детализации модели по назначению и характеру. При этом чем детальнее классификация, тем легче предпринять адекватное управление.

2. Повышением точности определения признаков при формировании модели, а значит снижением возможности ошибочных решений, часто опасных для управления (снижение ошибок классификации).

Чтобы результаты формирования были более приемлемы для последующего управления, приходится дополнительно к имеющимся m классам вводить (m +1)- й, когда отказываются от выбора, а значит и от управления. Отказ от управления лучше, чем управление при ошибочности выбора признака.

Для определения отношения между числом классов и ошибками распознавания рассмотрим одномерный случай. Пусть для вероятностного признака распознавания x заданы три класса объектов W ₁, W ₂, W ₃ распределениями вероятностей f (x | W ₁), f (x | W ₂), f (x | W ₃), априорными вероятностями P (W ₁), P (W ₂), P (W ₃) и матрицей потерь при решениях:

.

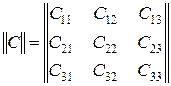Если априорная вероятность отнесения объекта к i -му классу, в то время как он принадлежит к j -му классу, равна P (W_i | W_j), то среднее значение платы за ошибочную классификацию всех m объектов в системе распознавания определяется как условная усредненная функция потерь (зависимость от Wj):

.

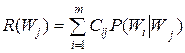В целом средние потери классификации определяются как среднее:

.

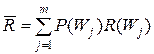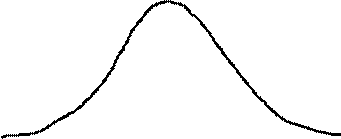
Остается определить вероятность P (W_i | W_j), так как априорное описание классов напрямую не дает ее значений. При этом классификация на базе функций плотности распределения вероятности параметра распознавания 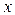для трех классов приведена на рис 4.2.

Если теперь определить области возможного разброса параметра распознавания каждого класса как G_i, то легко определить записанную нами вероятность ошибки так:

.

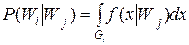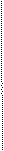
f (x | W_i)

f (x | W ₁) f (x | W ₂) f (x | W ₃)

a b X

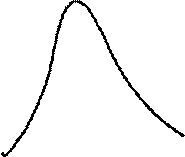
Рис. 4.2. Функции плотности распределения вероятности параметра распознавания 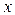для трех классов

Обозначим указанные области G_i на рисунке. Здесь эти области в силу одномерности случая должны представлять собой отрезки. Поэтому достаточно указать границы: а – граница между 1-м и 2-м классами; b – граница между 2-м и 3-м классами. Соответственно отрезки: 1-го класса ] – ¥, + a ]; 2-го класса ]+ a, + b ]; 3-го класса ]+ b, + ¥[. Теперь можно записать в соответствии с приведенной формулой условные риски ошибочных решений:

;

;

.

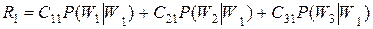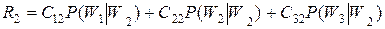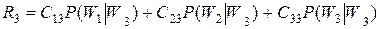Отсюда средний риск ошибочных решений в системе распознавания (то есть, риск ошибочной классификации всех классов):

.

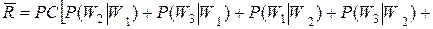
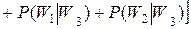Для простоты рассмотрения принимаем С_ii = 0, C_ij = C, P_i = P и, пользуясь рисунком, получим

.

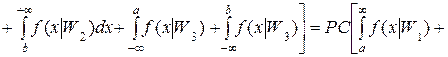
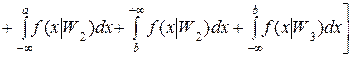Здесь обозначен средний риск индексом "1", так как теперь рассмотрим вторую ситуацию, для которой постараемся уменьшить число классов, объединяя первый и второй классы в один – четвертый.

Определим по правилам теории вероятностей ПРВ четвертого класса по ПРВ первого и второго классов:

.

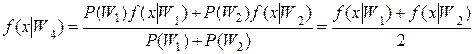До этого упрощали представление вероятностей и плат за ошибки для трех классов. Добавим к этому и четвертый класс:

;

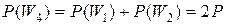C ₄₄=0; C ₁₄ = C ₄₁ = C.

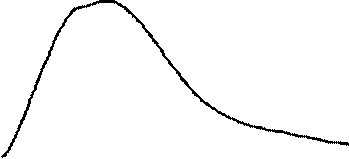
На рисунке плотности распределения вероятностей классов изобразим плотностью распределения вероятностей четвертого класса (пунктир).

Теперь можно записать, как и в первом случае (три класса), условные риски ошибочных решений для оставшихся 3-го и 4-го классов:

; .

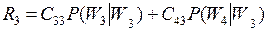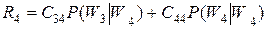Условные риски R ₁ и R ₂ здесь отсутствуют, так как произошло объединение 1-го и 2-го классов в 4-й. Кроме того, матрица плат за ошибки с учетом четвертого класса приняла сначала вид

,

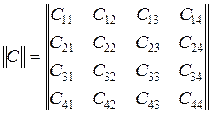а затем из нее за счет того же объединения исключили столбцы и строки, имевшие индексы "1" и "2". В результате получаем:

.

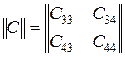Средний риск для случая двух оставшихся классов W ₃ и W ₄ обозначим индексом "2" и так же, как для первого случая, после простых преобразований получим

.

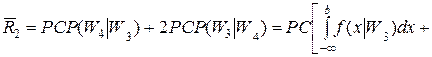
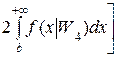Теперь, если подставим сюда вместо плотности распределения вероятности f (x | W ₄) его выражение, определенное уже нами, то получим

.

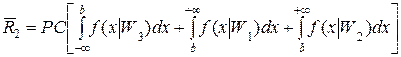Сравнив средний риск 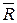₁ и 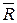₂, получаем

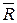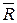₁ > ₂.

При заданном признаковом пространстве и прочих равных условиях уменьшение числа классов приводит к уменьшению ошибок выбора признаков, а при увеличении числа классов для уменьшения среднего риска (через уменьшение вероятности ошибочных решений) необходимо включать в состав словаря признаков такие, которые имеют меньший разброс.

Для установления взаимосвязи между размерностью вектора признаков и вероятности правильности формирования модели надо иметь в виду, что увеличение числа признаков модели должно приводить к повышению ее эффективности, так как рано или поздно в составе вектора может появиться такой признак, разброс которого минимален.

Для доказательства данного положения допустим, что:

– для каждого k -го признака измерения существует некоторая вероятность такого события A_k, когда решение о принадлежности объектов к W_i классу принимается;

– признаки измерения независимы между собой.

Независимость признаков означает и независимость событий A_k (событий принятия однозначных решений о принадлежности). Вероятность наступления двух совместных или несовместных событий A ₁ и A ₂:

P (A ₁ + A ₂) = P (A ₁) + P (A ₂) – P (A ₁ A ₂).

Для трех событий имеем

P (A ₁+ A ₂+ A ₃) = P [ A ₁+(A ₂+ A ₃)] = P (A ₁) + P (A ₂ + A ₃) – P [ A ₁ (A ₂ + A ₃)] =

= P (A ₁) + P (A ₂) + P (A ₃) – P (A ₂ A ₃) – P (A ₁ A ₂ + A ₁ A ₃) =

= P (A ₁) + P (A ₂) + P (A ₃) – P (A ₂ A ₃) – [ P (A ₁ A ₂) + P (A ₁ A ₃) – P (A ₁ A ₂ A ₃)]

или

.

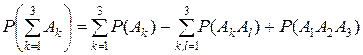Точно так же для четырех событий:

.

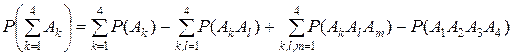Теперь образуем разность между вероятностями суммы 4-х и 3-х событий, состоящих в рассматриваемом случае в принятии однозначного решения о принадлежности по 4 и 3 признакам измерения соответственно:

.

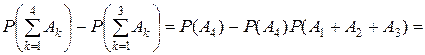
Наиболее просто эту разность получить, не доводя уменьшаемое до конечного вида

.

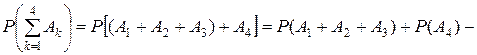
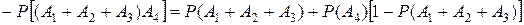Согласно принципа индукции можно записать:

.

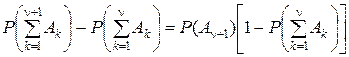Поскольку

,

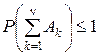то при любом значении n имеем

.

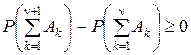Из данного выражения следует, что при увеличении числа признаков модели измерения увеличивается вероятность правильного ее формирования, т.е. ряд

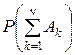
при 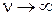монотонно возрастает и сходится. Для сходящейся последовательности

,

а значит

.

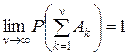Из полученного выражения следует

Теорема: Увеличение вероятности правильного формирования модели измерения может быть достигнуто за счет увеличения размерности вектора для независимых признаков, а при зависимых признаках (коррелированных) для этого можно дополнительно использовать связь между признаками, приводящими к лучшей разделимости классов.

Полученный результат можно достигнуть способами преобразования признаков модели измерения, которые сформулированы выше.

Дата добавления: 2014-01-05