Обоснование выбора критерия расхождения для формирования модели измерения по экспериментальным данным

Лингвистический алгоритм формирования модели измерения на начальных этапах оценивания

Использование аппарата математической лингвистики для описания структуры модели требует произведения сегментации области значений на составные части, т. е. выбора элементов для описания типичных фрагментов и методы их поиска. После предварительной работы, обеспечивающей выделение элементов, возникают собственно лингвистические задачи, состоящие из задач автоматического грамматического разбора описаний для распознавания изображений. Алгоритмы формирования модели, сводящиеся к выделению компактных множеств в заданных пространствах, определяют только абстрактные модели. Различие между геометрическим и лингвистическим алгоритмами состоит в формализации понятия компактности.

При измерении искомые подобласти, формируемые в процессе измерения по искомой модели измерения и соответствующие гипотезам H ₁ и H ₂, характеризуются равномерным законом распределения и в общем случае определяются на интервалах 0 £ x £q₁, d £ x £ d + q₂, q₁ < q₂. Учтя в выражении расхождения, полученном в задаче 3.3, начальное смещение d, получают новую смещенную на d область 0 £ x £ q₂, причем q₁ < q₂, тогда

I (1:2) = log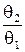+ d = (logq₂ – logq₁) + d = H_h (q₂) – H_h (q₁) + d, (5.1)

где H_h (q _i) – мера информации по Хартли разбиения соответствующей выборки.

Для случайной выборки О_n в n независимых квантов:

I (1:2; О_n) = n log+ d. (5.2)

Из полученного выражения для критерия следует, что расстояние между двумя множествами определяется разностью между мерами информации по Хартли и величиной сдвига интервалов определения каждого из множеств.

Разбиение области значений базируется на представлении измерительной процедуры, даваемой в теории измерений [66], заключающейся в следующем. Поскольку входное воздействие всегда имеет аналоговый характер, а результаты измерения представляются именованным числом, то в состав измерительной процедуры всегда входит аналого – цифровое преобразование. В связи с этим под измерительным преобразованием понимается преобразование, сводящееся к формированию числового эквивалента измеряемой величины в виде именованного числа, которое определяет ее интерпретацию как сравнение с функционально связанной с ней мерой, имеющей известное значение величины.

В метрологии различают два возможных метода сравнения: уравновешивание и сопоставление, в каждое из которых входит аналого – цифровое преобразование. Переход от аналоговых величин к их числовым эквивалентам требует выполнения дискретизации и квантования. Необходимость дискретизации обусловлена тем, что получаемый результат (числовой эквивалент) всегда соотносится с конкретным моментов времени и пространственными координатами, т.е. заключается в замене непрерывной функции j(r) в последовательность {j(r_s)}.

Полагая, что в качестве аргумента выступает время, дискретизацию можно представить следующим образом:

R j(t_s) = {j(t_s)} _{s =}= .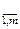

Простейший вариант – равномерное квантование, основан на разбиении диапазона возможных значений квантуемой величины на N_k одинаковых интервалов (квантов) G_s и сводится к определению, какому числу квантов соответствует входное воздействие. Формально операция квантования величины j Î [0, Ф_max] может быть представлена так:

R 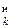j(t_s) = E ,

где Е [.] – целая часть [.]; D _k j = Ф_max/ N_k – интервал квантования.

При неравномерном квантовании определяющее его соотношение имеет вид

R 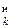j(t_s) = max j _i /j(t_s) ³ j _i,

т.е. в качестве результата квантования выступает значение максимального порогового уровня, для которого выполняется неравенство j(t_s)³j _i (здесь j _i – верхние границы квантов, i = 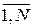). Размер s -го кванта при неравномерном квантовании определяется разностью G_s = j _s – j _{s –1}.

При этом полученное разбиение является достаточным разбиением для различения, поскольку полученные при разбиении кванты содержат в себе такую же информацию, как разбиение с элементами в виде точек исходного пространства и, следовательно, информация при разбиении не теряется.

Причем величина кванта определяется:

– принципиальной непознаваемостью, обусловленной свойствами материи – неисчерпаемостью микроструктуры и неопределенностью текущего состояния;

– ограниченностью возможностей эталонной базы (системы обеспечения единицы измерений);

– неадекватностью модели реальному объекту, ибо величина отображает свойства физического объекта как характеристику его модели.

При достаточном уровне избыточности исходных данных проектирования, разбив весь диапазон возможных значений измеряемой величины, можно построить множество допустимых вариантов квантов çГ₀ç. Множество Г₀, полученное в результате квантования, является конечным, но количество его элементов çГ₀ç зависит от точности и избыточности исходных данных синтеза.

Описанные алгоритмы обеспечивают формирование начальной модели измерения, которая содержит основные структурные свойства исходных оцениваемых результатов измерения и поэтому могут быть использована для сокращения трудоемкости подробного структурного анализа.

Дата добавления: 2014-01-05