Метод формирования модели измерения

Если предположить, что результаты измерения, входящие в область значений пространства признаков, формируются, исходя из искомой ММИ, то можно принять, что задание пространства признаков само по себе определяет свойство, под действием которого область значений ММИ в этом пространстве легко разделяется, т.е. взаимное расположение точек в выбранном пространстве уже содержит информацию о разделимости переменных синтезируемой ММИ, которая оказывается достаточной для формирования модели. Данное условие формирования ММИ можно сформулировать в виде гипотезы компактности, по которой ММИ соответствуют компактные множества, составляющие область ее значений в пространстве признаков. Сформированные при этом множества ММИ, которым в абстрактном пространстве соответствуют компактные множества точек, разумно назвать абстрактными ММИ данного пространства.

Воспользовавшись аппаратом математической лингвистики и сформулированной гипотезой компактности, можно описать структуру ММИ, для чего требуется осуществление сегментации области значений на составные части, то есть выбор элементов для описания типичных фрагментов и методы их поиска. После предварительной работы, обеспечивающей выделение элементов, возникают собственно лингвистические задачи, состоящие из задач автоматического грамматического разбора описаний для распознавания ММИ. Алгоритмы формирования модели, сводящиеся к выделению компактных множеств в заданных пространствах, определяют только абстрактные модели. Различие между геометрическим [85] и лингвистическим подходами при синтезе алгоритмов состоит в формализации понятия компактности. Сформулированная гипотеза компактности позволила синтезировать критерий для сравнения качества данных моделей и, как следствие, качество алгоритма синтеза ММИ, формализованный выбор которого осуществлен в работе [5].

Синтез метода и алгоритма формирования модели измерения на начальном этапе измерения. Метод формирования ММИ, использующий лингвистический подход при его синтезе, предназначен для использования на ранних этапах оценивания и основан на анализе множества допустимых вариантов оцениваемого параметра [86]. Данный метод формирования ММИ на начальных этапах оценивания предусматривает последовательное выполнение следующих этапов:

1. Выбор произвольного числа r квантов из множества Г₀, которые отличаются друг от друга сильнее, чем все остальные невыбранные кванты, т.е. нахождение такого подмножества ГÍГ₀ с количеством элементов çГç= r £çГ₀ç, для которого выполняется условие

[" G_i, " G_j (G_i, G_j Î Г) & " G_k, " G_l (G_k, G_l Î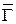)]: I_ij ³ max(I_ik, I_kl),

где I_ij, I_ik, I_kl – степени различения квантов G_i c G_j, G_i с G_k, G_k с G_l.

2. Кластеризация выбранных в п. 1 квантов на непересекающиеся кластеры, объединяющие однотипные кванты и имеющие максимальное расстояние между кластерами. Формально это значит разделение множества Г на непересекающиеся множества Г₁, Г₂, …, Г _s, где 1 £ s £ r с учетом выполнения условия

[" G_i, " G_j (G_i, G_j Î Г _m) & (" G_k Ï Г _m)]: I (G_i, G_j) < I (G_i, G_k),

где Г _m Í Г, m = – m -й кластер множества Г, I (G_i, G_j) – расстояние между квантами G_i и G_j. Причем 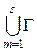_m = Г, а = Æ.

3. Формирование ММИ G на базе кластеров Г _m, m = таким образом, чтобы центр кластера отражал характерные свойства элементов множества Г _m = (G_{m 1}, G_{m 2}, G_mn), т.е. определение

G = F (G_{m 1}, G_{m 2}, G_mn), m = .

Таким образом, в результате решения трех данных задач из множества допустимых вариантов квантов Г₀, имеющего огромное количество элементов, получаем ММИ, которая определяется небольшим количеством типовых элементов 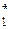(G 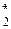, G ,…, G ), рассматриваемые как переменные ММИ. Если некоторая типовая переменная модели G по результатам метода явно превосходит остальные, то оптимальный вариант ММИ целесообразно искать в близости G , т.е. в кластере Г _m:

I. Выбор множества максимально различающихся квантов Г*, может быть осуществлен с помощью алгоритма, который сортирует элементы множества Г₀ и отбрасывает мало отличающиеся. Для вычисления различия квантов можно использовать выражение (5.1), полученное по результатам решения задачи 2.3, которое позволяет оценить степень различия как двух квантов, так и множества квантов, составляющих область значений. Степень различия I _ij выражает отличия квантов G_i и G_j и находится в интервале [0, 1+ d ]. При I_ij =0 кванты G_i и G_j изоморфны, а при I_ij =1+ d они не совпадает, то есть G_{i 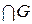j} =Æ. Поскольку алгоритм отбора просматривает огромное число квантов для их сравнения, а хранение в памяти ЭВМ всех элементов множества Г₀ нецелесообразно, поэтому алгоритм отбора ориентирован на последовательный анализ допустимых вариантов ММИ, которые сразу после выбора сравниваются с отобранными, а в памяти ЭВМ сохраняется только множество Г*.

II. Второй этап алгоритма формирования ММИ на ранних этапах оценивания – этап кластеризации квантов, который выполняется с помощью алгоритма максиминного расстояния. Расстояние I (G_i, G_j) между квантами G_i и G_j определяется выражением (5.2) с учетом смещения d между квантами.

Для выбора значения d принимается компромиссное решение между точностью рассчитываемого расстояния и требуемым машинным временем для нахождения множеств.

Задачу кластеризации элементов множества Г можно рассматривать как разбиение Г на s непересекающихся подмножеств Г₁, Г₂, …, Г _s, для которых произвольный элемент r_i вектора 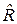= (r ₁, r ₂, …, r_s) указывает мощность подмножества Г _i çГ _i ç = r_i, где 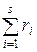= r = çГç, а элемент v_i вектора 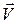= (v ₁, v ₂, …, v _s) выражает текущее количество элементов множества Г _i во время выполнения алгоритма. Первый элемент произвольного кластера Г _i называется центром и обозначается G_{i 1} Î Г _i.

III. Формирование ММИ G 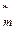на базе кластеров Г _m, m = 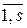позволяет значительно сократить трудоемкость проведения подробного структурного анализа, так как типовой квант G 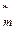содержит основные структурные свойства квантов соответствующего кластера Г _m ={ G_{m 1}, G_{m 2}, G_mrm }, поэтому отпадает необходимость анализа всех его элементов. Результатом задачи формирования ММИ является определение множества кластеров Г 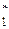^* ={ G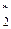 , G, G }, свойство каждого из которых определяется его центром. При этом начальную ММИ на базе G 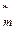Î Г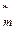получают, объединяя элементы множества Г _m, в виде переменных ММИ, то есть

(" m = 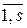): G = .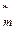

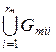Описанные алгоритмы обеспечивают формирование начальной ММИ, которая содержит основные структурные свойства исходных оцениваемых результатов измерения. Форма представления данных и структура алгоритмов ориентированы на их программную реализацию и включение в состав разработанной диалоговой системы оценивания результатов измерения.

Дата добавления: 2014-01-05