
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение задачи. Типовые задачи и примеры их решения
|
|
|
|
Типовые задачи и примеры их решения
Задача 5.1. Реализовать алгоритм выбора множества максимально различающихся квантов Г*.
Итеративный алгоритм выбора множества Г* (рис. 5.2) состоит из этапов:
1. Устанавливается количество необходимых максимально отличающихся квантов Г*, т.е. количество элементов множества Г*. При этом необходимо учитывать неравенство r £ çГ0ç, а также вычислительные ресурсы (память и машинное время), имеющиеся для синтеза, отбора и структурного анализа вариантов.
2. Формируется первое приближение Г( i ), i = 1 множества Г, в которое включаются первые r 2 элементы множества Г0.
3. Устанавливаются начальные значения счетчика рассмотренных квантов t =0, порогового значения степени различия g0=0, а также константа e, задающая необходимую точность расчетов.
4. Вычисляется средняя степень различия g i квантов множества Г( i ):
g i = 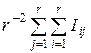 , i ¹ j. 2.
, i ¹ j. 2.
5. Если g i – g i –1 < e, то переходим к п. 10 (конец алгоритма).
6. Увеличивается значение t = t + 1 для рассмотрения следующего элемента множества Г0, которое обозначается Gr + t.
7. Если r + t ³ çГ0ç или израсходовано машинное время, отведенное для выбора вариантов квантов, то переходим к п. 10 (конец алгоритма).
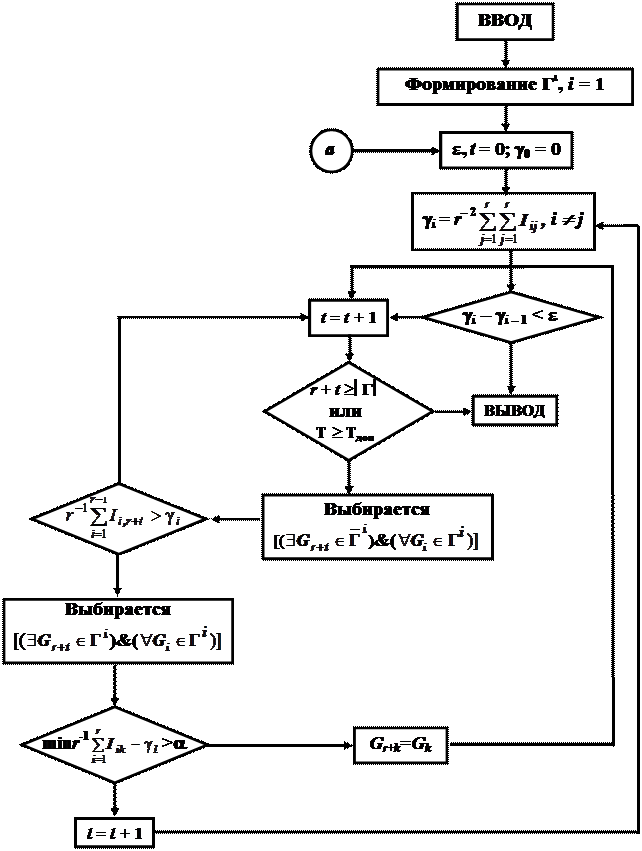
Рис 5.2. Алгоритм формирования множества максимально различающихся квантов
8. Квант Gr + t попарно сравнивается со всеми квантами Gi Î Г( i ) по выражению (5.1). Если выполняется условие
[($ Gr + t Î 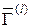 )&(" Gi Î Г( l ))]:
)&(" Gi Î Г( l ))]: 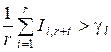 ,
,
где 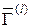 – дополнение Г( l ) до множества Г0, то переходим к следующему пункту. В противном случае – переходим к п. 6.
– дополнение Г( l ) до множества Г0, то переходим к следующему пункту. В противном случае – переходим к п. 6.
9. В множестве Г( i ) находится квант Gk, который максимально подобен остальным элементам множества Г( i ), т.е. Gk, для которого выполняется условие
[($ Gk Î Г( i )) &(" Gi Î Г( i ))]: 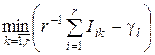 <0.
<0.
Если квант Gk найден, то в дополнение Г( l ) вместо него включается квант Gr+k и осуществляется переход к п. 6. В противном случае получено (l +1)-е приближение Г( l +1) множества Г, поэтому увеличивается l = l + 1 и осуществляется переход к п. 4.
10. Конец алгоритма.
В данном алгоритме постепенно увеличивается пороговое значение степени подобия g l, которое используется для принятия решения при отборе вариантов квантов. Прерывается выполнение алгоритма в любой момент времени. При этом в множестве Г( i ) содержатся наиболее различающиеся кванты из r + t квантов, рассмотренных до момента прерывания.
Задача 5.2. Реализовать алгоритм кластеризации квантов.
Решение задачи. На рис. 5.3 приводится алгоритм максиминного расстояния, предназначенный для кластеризации допустимых вариантов формирования областей определения X исходной области значений Y:
1. Устанавливаются начальные значения вектора текущего количества элементов кластеров 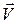 = 0, текущего количества кластеров p = 2 и количества кластеризованных квантов, не являющихся центрами кластеров t = 0. Подмножества Г i Ì Г в начале алгоритма пусты и постепенно пополняются квантами из множества Г.
= 0, текущего количества кластеров p = 2 и количества кластеризованных квантов, не являющихся центрами кластеров t = 0. Подмножества Г i Ì Г в начале алгоритма пусты и постепенно пополняются квантами из множества Г.
2. В множестве Г* ищется пара квантов Gp 1, Gp –1,1, для которой:
[($ Gp 1 Î Г*) & ($ Gp –1, 1 Î Г*)]: I (Gp 1, Gp –1,1) = 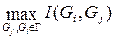 ,
,
где I (Gi, Gj) – расстояние между квантами Gi и Gj определяемое по выражениям (5.1, 5.2).
|
|

|





|



|

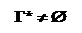


|


|
|
|


|
|
|
|

|



|

|

Рис. 5.3. Алгоритм кластеризации квантов
3. Найденные кванты назначаются центрами для двух первых кластеров Г1 и Г2, т.е. формируются текущие варианты множеств 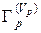 ,
, 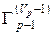 и
и 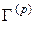 на базе предыдущих их вариантов
на базе предыдущих их вариантов 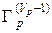 ,
, 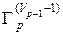 и
и 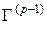 по выражениям
по выражениям
Vp –1= Vp –1+1; 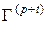 =
=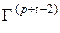 |{
|{ };
}; 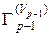 =
=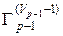 U{ Gp –1,1}.
U{ Gp –1,1}.
4. Vp = Vp +1; 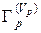 =
=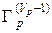 U{ Gp 1}; p = p +1.
U{ Gp 1}; p = p +1.
5. Среди оставшихся элементов множества Г ищется квант Gp 1, для которого выполняется условие
($ Gp 1 Î Г): 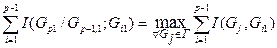 .
.
6. Найденный квант исключается из множества Г, т.е.
Г( p + t ) = Г( p + t –1)|{ Gp 1}.
7. При выполнении условия
(" i =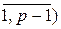 :
: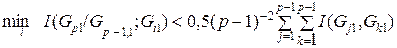 = Im,
= Im,
квант Gp 1 (Gp –1,1) обозначается GiVj и включается в ближайший кластер Г j, т.е. Vj = Vj + 1; Г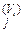 = Г
= Г U{ GiVj }; t = t + 1, и переходим к п. 8, а в противном случае к п. 9.
U{ GiVj }; t = t + 1, и переходим к п. 8, а в противном случае к п. 9.
8. Проверяется количество рассмотренных квантов. Если p + t ³ r, то переходим к п.13 (конец алгоритма), в противном случае к п. 5.
9. Найденный квант включается в переходное множество Г¢, в котором накапливаются кванты, не вошедшие в уже сформированные кластеры, т.е.
Г¢ = Г¢U{ Gp -1, i }.
10. Если множество Г* ¹ Æ, то переходим к п. 5. В противном случае переходим к следующему пункту.
11. Среди сформированного переходного множества Г¢ ищется квант Gj 1, для которого выполняется условие
($ Gj 1 Î Г¢): 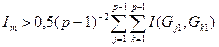 .
.
Найденный квант Gj 1 назначается центром нового кластера и переходим к п.13. В противном случае переходим к следующему пункту.
12. Сформированное множество Г¢ объявляется множеством Г, то есть выполняется условие Г = Г¢, а p = p + 2, и переходим к п. 2.
13. Конец алгоритма.
Описанный алгоритм выполняет кластеризацию структур Gi ÎГ с автоматическим выбором количества кластеров s, где 2£ s £ r. В любой момент выполнения алгоритма 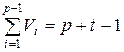 . В конце алгоритма s = p, а
. В конце алгоритма s = p, а 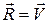 . Преимуществом алгоритма является кластеризация без повторного пересмотра элементов.
. Преимуществом алгоритма является кластеризация без повторного пересмотра элементов.
Задача 5.3. Реализовать алгоритм формирования переменных модели измерения.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 335; Нарушение авторских прав?; Мы поможем в написании вашей работы!
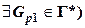 &(
&(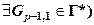 ]: I (Gp 1, Gp -1,1) =
]: I (Gp 1, Gp -1,1) = 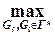 I (Gi, Gj)
I (Gi, Gj)
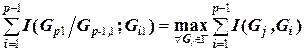
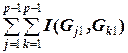 =
= Im
=
= Im