Синтез метода и алгоритма формирования стратегии постановки начальных экспериментов

Кроме рассмотренного в предыдущем параграфе метода формирования ММИ, качество оценивания результатов измерения определяется также и правильно выбранным методом формирования стратегии эксперимента, порождающего данные результаты измерения. В связи с этим перейдем к рассмотрению вопроса синтеза стратегии эксперимента, обеспечивающего максимальное качество оценивания результатов измерения на первоначальном этапе исследования объекта в условиях отсутствия априорной информации.

На первоначальном этапе исследования объекта, при отсутствии априорной информации измерения, синтеза стратегии эксперимента не может быть осуществлен стандартными методами синтез стратегии эксперимента, порождающего наблюдение Y [3]. Однако системный подход к постановке эксперимента позволяет синтезировать стратегию эксперимента на основе всестороннего систематизированного изучения данной проблемы в целом при учете внешних и внутренних связей, элементов, закономерностей функционирования контролируемого объекта [5].

Концептуальная модель постановки начального эксперимента. При постановке начального эксперимента, для получения исходной для анализа информации измерения, возможно применение логико - лингвистического подхода, опирающегося на априорные данные и логику процесса управления [85, 90] и использующего общие принципы системного подхода. При этом целесообразно использовать принцип чувствительности, который сводится к тому, что вмешательство в контролируемый объект должно согласовываться с уровнем ее реакции на вмешательство, а также принцип неопределенности, в соответствии с которым учет неопределенностей и случайностей в системе осуществляется посредством введения границы вариации переменных:

y – D_п y ¸ y + D_п y, – D_п¸ + D_п, u – D_п u ¸ u + D_п u.

В соответствии с принципами системного анализа, сущность стратегии управления первоначальным экспериментом можно сформулировать в виде следующего высказывания: “Если заданное состояние объекта y (t) характеризуется скоростью изменения состояния (t), то назначается управляющее воздействие u (t)”. Данное логическое условие постановки управляющего эксперимента можно представить в виде алгебраического отношения, причем априорная непредсказуемость локальных изменений параметра y (t) и (t) делает это отношение нечетким. Набор таких нечетких отношений [85] образует нечеткий алгоритм и является нечеткой моделью управляемого процесса.

Модель статистического эксперимента. Математическая модель статистического эксперимента, принятая в §2.1 в соответствии с работой [3], может быть представлена в виде

x (u) = j(b (u), w),

а структура данного стохастического эксперимента приведена на рис.5.1.

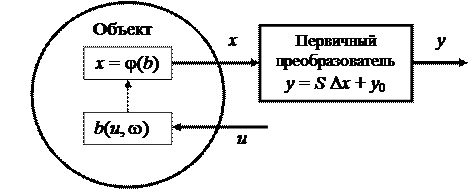
Рис. 5.1. Структура статистического эксперимента

Причем, если функция преобразования объекта j(b) непрерывна и каждому значению b случайной величины B соответствует одно значение x случайной величины X и наоборот, то плотность распределения случайной величины x [96] равна

f (x) = b (y(x), w)|y¢(x)|,

где y(x) – обратная функция для j(b).

В общем случае, математическую модель оценивания результатов измерения, т.е. систему математических соотношений, описывающих оцениваемые и контролируемые параметры, в соответствии с принятой концептуальной моделью эксперимента можно представить в следующем виде:

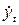= q (y_t) + w_t;

y_t = h (x_t) + v_t,

где q (x_t) и h (x_t) – нелинейные известные функции, аргументом которых служит оцениваемый параметр x_t; w_t и v_t – случайные процессы, являющиеся функциями времени t.

Для конкретизации данной модели учтем, что начальный этап исследования контролируемого объекта характеризуется полным отсутствием априорных сведений о возможных значениях параметров контролируемого объекта в задаче оценивания. Причем математический результат, предназначенный для практического использования, должен обладать свойством устойчивости по отношению к небольшим отклонениям от исходных предположений. Однако в ряде случаев даже небольшие вариации исходных предпосылок о вероятностной структуре информации измерения могут привести к существенному ухудшению свойств используемых процедур, что определяет необходимость использования робастного подхода при оценке в этом случае результатов измерения.

Робастная процедура обработки может несколько уступать в эффективности процедуре, которая для этой модели оптимальна, но зато полная эффективность для данного класса моделей будет высокой или, по крайней мере, достаточной. При решении задачи оценивания ищется процедура обработки результатов измерения, которая в наихудшем случае обладает оптимальной эффективностью, что приводит к минимаксным робастным алгоритмам. При робастном подходе, для задания наихудших условий в задаче оценивания результатов измерения, целесообразно использовать случайные процессы w_t и v_t с нормальным законом распределения, который обладает экстремальным свойством [96], поскольку среди всех случайных величин, имеющих одну и ту же дисперсию, наибольшей энтропией обладает нормально распределенные случайные величины. При этом первичный преобразователь в детерминированном случае может быть, в соответствии с работами [111, 68], представлен в виде

y = S D x + y ₀,

где y ₀ – начальное значение выходного параметра (нулевой уровень); S – чувствительность преобразователя.

В общем случае чувствительность преобразователя является нелинейной функцией, однако обычно стремятся иметь линейную характеристику преобразования, т.е. прямую пропорциональность между изменением входной величины и соответствующим приращением выходной величины преобразователя. Если S нелинейная функция, то при этом происходит группировка, сгущение или другие преобразования наблюдений. В результате изменяется плотность распределения выборки, сформированной на выходе первичного преобразователя, что искажает информацию о измеряемом параметре, которая сформировалась на выходе объекта, и приводит, в общем случае, к потере информации о измеряемом параметре. Причем достаточность статистики для семейства распределений не нарушается при усечении или при отборе.

Таким образом, существуют интервалы функции преобразования объекта, которые можно рассматривать как линейные участки, и на этих участках будет формироваться соответствующий информационный уровень. При переходе на другой интервал функции преобразования объекта на выходе контролируемого объекта будет формироваться выходная величина x, плотность распределения которой будет отличаться от плотности распределения на предыдущем интервале. Данное изменение плотностей распределения формирует информацию на выходе контролируемого объекта, которая определяется свойствами контролируемого объекта. Оценка этой информации и является целью процесса измерения. Однако при измерении аналогично будет изменяться и плотность распределения на выходе первичного преобразователя, в соответствии с интервалами линеаризации его функции чувствительности, но в этом случае данные изменения приводят к потере первичной объектной информации о свойствах контролируемого объекта. Поэтому целесообразно в качестве первичного преобразователя использовать преобразователь с линейной характеристикой преобразования.

Для анализа сходства входной и выходной информации первичного преобразователя и выяснения того, что информация не теряется, необходимо сформировать критерий оценивания результатов измерения как критерий различия между разными плотностями.

Формирование критерия оценивания результатов измерения. Пусть имеется задача статистического решения, состоящая в определении по совокупности данных наблюдения по единичным измерениям, сопровождающимся случайными ошибками. Как известно [94], для оценивания результатов измерения можно выделить несколько вариантов задачи оценивания. Причем решение рассматриваемой задачи оценивания на начальном этапе исследования контролируемого объекта в условиях отсутствия априорной информации невозможно искать в виде задачи интерполяции (t <t) и задачи фильтрации (t =t), требующих априорную информацию достаточного объема.

Полное отсутствие априорных сведений о возможных значениях параметров контролируемого объекта в задаче оценивания приводит к необходимости ее постановки в виде задачи экстраполяции (t > t), характеризующейся минимальной априорной информацией, которая определяется лишь только начальным состоянием контролируемого объекта. Будем считать изменение состояния контролируемого объекта линейным, так что его текущее состояния y (t) есть

y (t) = y ₀ + t,

где y ₀ – состояние объекта в начальный момент времени t = 0. Конечной целью является определение состояния объекта при начальном состоянии y ₀ и скорости – и вычисление по их значениям положения объекта

y _э = y ₀ + t _э, (5.3)

экстраполированного на некоторый момент времени t _э, исходя из требования минимума квадрата отклонения оценки экстраполированного положения от истинного значения этого положения.

В силу линейности (5.3) относительно y ₀ и , оптимальная оценка экстраполированного состояния y _э в виде математического ожидания, при квадратичной функции потерь, имеет вид

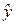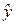_э = ₀ + 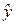t _э, (5.4)

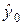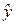где и – оптимальные оценки (условные математические ожидания при фиксированной совокупности данных наблюдения) параметров y ₀ и .

Конечное требование минимума среднего квадрата отклонения оценки экстраполированного состояния от истинного значения, сводится к нахождению оптимальных оценок параметров y ₀ и и формированию оценки 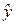в соответствии с элементарным правилом (5.4). Причем для оценки параметров y и = 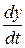в виде математических ожиданий [88] имеем

= .

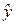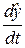Минимальный апостериорный риск конечного решения – выбора в качестве оценки экстраполированного положения величины 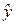из равенства (5.4) – определяется очевидным соотношением

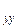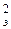R _min = S _yy + 2 t _эS + t S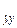, (5.5)

где S _yy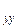, S , S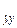– соответствующие элементы апостериорной корреляционной матрицы параметров y ₀ и .

Для получения оценок параметров y ₀ и имеется возможность произвести N единичных измерений х_v, (v =1,..., N) в моменты времени t ₁ = 0, t ₂ = D t, ..., t_N = (N – 1)D t, причем на данном v -м шаге может быть произведено единичное измерение текущего значения координаты объекта:

x_y = y (t_v) + x _v = y ₀ + t_v + x _v,

где x _v – случайная нормально распределенная величина с нулевым математическим ожиданием и дисперсией s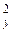и единичное измерение скорости объекта:

x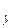 = + h _v,

где h _v – случайная нормально распределенная величина с нулевым математическим ожиданием и дисперсией s.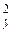

Таким образом, мы имеем многошаговый управляемый процесс измерения, в котором конечный средний и минимальный по конечному решению апостериорный риск (5.5) зависят от последовательности решений u ₁, и ₂ ,..., u_{n –1}, определяющих порядок получения данных наблюдения. Фактически эти риски зависят только от номера шага п. При этом

R _min = R _min(n) = S _yy (n) + 2 t _эS 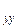(n) + t 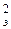S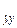(n), (5.6)

где S _yy (n), S 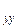(n), S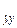(n) – элементы апостериорной корреляционной матрицы параметров y ₀ и при условии, что сначала произведено n замеров текущего значения координаты. Для нахождения оптимального правила решения в целом достаточно найти минимум (5.6) по п.

Полному отсутствию априорных сведений о возможных значениях параметров y ₀ и в рассматриваемой задаче экстраполяции эквивалентно тому, что априорный разброс значений y ₀ и велик, по сравнению с апостериорным, при любом выборе значения n. В этом случае апостериорная корреляционная матрица параметров y ₀ и совпадает с матрицей обратной, взятой с противоположным знаком матрице вторых производных по этим параметрам от логарифма функции правдоподобия:

P (x ₁,..., x_n | y ₀, , n)=´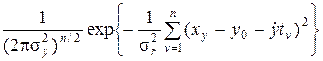

´.

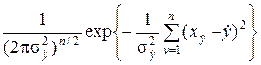Для определения величины риска для данной функции правдоподобия составим информационную матрицу Фишера, которая в гильбертовом пространстве функций L ₂(v), интегрируемых с квадратом относительно меры v на X, со скалярным произведением (j, y) = 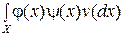и нормой 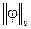, имеет вид

I (q) = 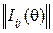= 4.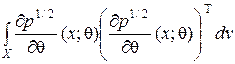

Если эксперимент Ĕ, который порожден случайным k - мерным вектором X и имеет плотность распределения в R^k, причем каждый элемент характеризуется гауссовским законом распределения со средним a и дисперсией D, то данный эксперимент регулярен, а

I (q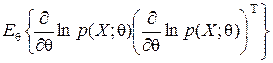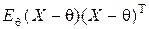) = = R ^–1 R ^–1,

так как 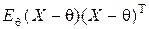= R.

Данной функции правдоподобия, благодаря нормальному распределению ошибок единичных измерений x _v и h _v, которые считаются независимыми для различных шагов, соответствует информационная матрица Фишера:

,

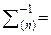
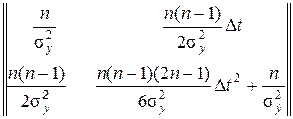откуда после обращения и подстановки в формулу (5.4) получим выражение для риска:

R _min(n)=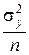+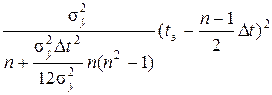, n = 1, 2,..., N.

Анализ данного выражения показывает, что величину риска по результатам измерения в нем можно определить условиями проведения эксперимента, в котором будет формироваться выборка данных. Для упрощения данного выражения, примем в нем второе слагаемое равным нулю. В этом случае получаем условие для формирования спектра эксперимента, при постановке которого может быть использована лишь только информация о состоянии контролируемого объекта, в виде условий проведения замеров в точках

t _э = 0,5(n – 1)D t,

причем качество получаемой оценки состояния объекта по результатам измерения определяется минимальным риском

R _min(n) = .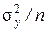

Алгоритм постановки начального эксперимента. Проведенный информационный анализ формирования достаточной статистики разбиения, приведенный в задаче 2.3, позволил сформировать критерий сравнения выходной информация для минимизации ее потерь при преобразовании. В качестве этого критерия сравнения необходимо использовать функционал расхождения, определяющий статистическое различие между сравниваемыми элементами выборки, которые получены в статистическом эксперименте.

Для того чтобы сформулировать алгоритм постановки начального эксперимента, введем основные построения. Пусть задано непрерывное пространство переменных Y, 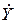, соответственно характеризуемых величинами заданного состояния объекта управления и скорости изменения этого состояния. Пусть также задано множество управлений U. Построим отображения F: S ® U следующим образом:

1. Разобьем области изменения аргументов Y и 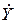на n подмножеств. Смысл этих разбиений заключается в определении с требуемой точностью результатов измерения по синтезированному плану эксперимента, причем как для положительных, так и для отрицательных значений спектра плана.

Для определенности эти подмножества будем обозначать:

A_i, i = 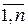; B_j, j = 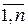, где A_i Ì Y, B_j Ì .

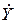2. Введем, в соответствии с моделью статистического эксперимента, функции b_Ai (y (u), w) и b_Bi ((u), w), отражающие при фиксированном значении параметра u Î U случайный характер реализации условий проведения эксперимента, где w – элементарное событие из W при заданной s-алгебре F и вероятностной мере P, для элементов y Î Y, Î 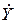, на выделенных подмножествах.

3. Каждому значению функций b_Ai (y (u), w) и b_Bi ((u), w) поставим в соответствие некоторые области изменения аргументов Y и 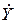, пересечение которых образует в пространстве S некоторую область s_ij Î S.

4. Аналогичные пунктам 1 и 2 построения выполним и для области изменения аргумента управления U. Смысл этих разбиений C_k, k = 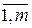, где C_k Ì U, заключается в задании с требуемой точностью плана эксперимента, для положительного (отрицательного) значения спектра синтезируемого плана эксперимента. Функции b_Сk (u) соответствует конкретное управляющее воздействие.

5. Каждой области s_ij Î S поставим в соответствие приведенное подмножество C_k Ì U изменения аргумента управления.

6. Множество приведенных областей s_ij Î S образует пространство управляемых параметров, которое удобно представить матрицей M = 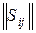ранга n ², тогда действие оператора отображения F будет заключаться в поиске для пространства M такого управляющего воздействия C_k, которому соответствует максимальное значение функции b_Сk (u).

Дата добавления: 2014-01-05