Системы с потерями

Рассмотрим основные показатели СМО, характеризующие качество работы

1. P_n – вероятность отказа, все пункты обслуживания заняты. Вероятность отказа

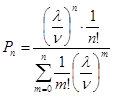2. P₀ — вероятность того, что в системе все аппараты свободны

3. P_k –вероятность ого, что в системе занято k аппаратов

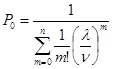4. P_n – характеризует полноту обслуживаня вхдящего потока, поэтому на практике часто пользуются модификацией этого показателя — средний процент отказа системы в обслуживании.

5. M — среднее число аппаратов пункта обслуживания.

~~~~~~~~~~~~~~~~~~~

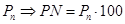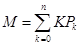Математическое ожидание требований за единицу времени (лямбда)

(ню) — математическое ожидание числа требований, обслуживаемых за единицу времени.

m — количество требований.

Pn — вероятность отказа.

Pk — вероятность того, что k аппаратов занято.

PN *100 — процент отказа.

Эти показатели в совокупности позволяют оценить качество функционирования СМО с потерями, как с точки зрения удовлетворения потока требований, так и с точки зрения полноты использования оборудования.

Известно, что для систем с потерями:

ф1

причем число требований не может быть больше числа аппаратов, поэтому целесообразно исключать из расчетов m, т.е. Вычислять P0 косвенно, через формулу (8), для этого подставить (5) в (8):

ф2

СМО с очередью характеризуется следующими показателями:

- P'_k — вероятность того, что в системе находится k требований, при этом число требований не превышает числа параметров, определяется зависимостью:

ф3

- P''_k — вероятность того, что в системе образовалась очередь, при этом число требований k больше числа аппаратов n. Описывается зависимостью:

ф4

- M1 — средняя длина очереди представляет собой среднее число требований, находящихся в очереди и ожидающих начало обслуживания:

ф5

- M2 — среднее число требований, находящихся в системе (в очереди и в пункте обслуживания):

ф6

- Т_ож — среднее время пребывания в очереди до начала обслуживания. Этот показатель является основным, так как показывает величину не производительной потери времени требования на пребывание в очереди. Очевидно СМО функционирует лучше, когда этот показатель меньше:

ф7

Последние 5 показателей определяют качество СМО с ожиданием. Кроме этих показателей СМО с ожиданием могут иметь практическое значение ряд вспомогательных показателей, таких как:

- Коэффициент простоя в очереди

ф8

- Коэффициент пребывания требования в системе в целом

ф9

Эти показатели позволяют сопоставить по эффективности СМО, имеющие различные входящие потоки и пункты обслуживания. Также как и для СМО с потерями, для СМО с ожиданием справедливо:

ф10

Подставим в (16) выражения (11) и (12):

ф11

При изменении k от 0 до m выражение (17) примет вид:

ф12

Таким образом выражения (3)-(20) являются математической моделью функционирования СМО, а также формулировкой решения задачи, определения основных характеристик СМО.

Выражениями (3)-(20) описываются как задачи анализа в результате решения которых определяются показатели функционирования существующих СМО, так и задачи синтеза в ходе решения которых определяется, каким параметром должны отвечать элементы, создаваемые СМО, чтобы она обеспечивала заданные задачи.

Условимся различать задачи анализа и синтеза:

- Z1 — анализ

- Z2 — синтез

Входными данными для задач синтеза СМО с потерями являются (лямбда), (ню), PNZ — заданный процент отказа.

Выходными данными для задач синтеза СМО: PN, n, M.

Дата добавления: 2014-01-05