Дробный факторный эксперимент (ДФЭ)

Количество опытов в ПФЭ значительно превосходит количество определяемых коэффициентов линейной модели. Другими словами, ПФЭ обладает большой избыточностью опытов. В таблице 2 показано соответствие количества факторов количеству экспериментов в ПФЭ.

Таблица 2 – Зависимость количества экспериментов (n) от количества факторов (к)

к
n

Необходима минимизация опытов. Количество опытов резко сокращается при использовании дробных реплик от ПФЭ, т.е. дробного факторного эксперимента.

Эксперимент, в котором применяется лишь некоторая часть сочетаний уровней факторов, в отличие от ПФЭ, называется дробным факторным экспериментом (ДФЭ).

Для того чтобы дробная реплика представляла собой ортогональный план, в качестве реплики следует брать ПФЭ для меньшего количества опытов. Количество опытов при этом должно быть большим или равным количеству коэффициентов в уравнении регрессии.

(к+ 1)£ n < 2^k

Допустим, что надо получить математическую модель для трехфакторного процесса (n =2³ = 8).Для решения этой задачи можно ограничиться четырьмя опытами, если в матрице планирования для ПФЭ 2² использовать столбец x₁x₂ в качестве плана для x₃ (таблица 3). Построим расширенную матрицу планирования экспериментов, т.е. матрицу, содержащую столбец взаимодействия факторов (x₁x₂).

При варьировании факторов на двух уровнях можно получить полином первого и неполного высшего порядка, то есть результаты эксперимента можно представить в виде неполного квадратичного уравнения:

Y = b₀ + b₁x₁ + b₂x₂ + b₁₂x₁x₂ (20)

Таблица 3 – Расширенная матрица планирования экспериментов

n	х0	х 1	х2	х1 х2
	+1	-1	-1	+1
	+1	+1	-1	-1
	+1	-1	+1	-1
	+1	+1	+1	+1

Если имеется основание считать, что в выбранных интервалах варьирования процесс может быть описан линейной моделью, то достаточно определить 3 коэффициента в ₀ , в ₁ , в ₂.

Остается одна степень свободы. Употребим ее для минимизации количества опытов.

Предположим в ₁₂ 0 и столбец х₁х₂ можно использовать для нового фактора х₃, т.е. заменим x₁x₂ на x₃.,элементы столбца при этом не изменяются. В результате этих преобразований получаем математическую модель следующего вида:

Y = b₀ + b₁x₁ + b₂x₂ + b₃x₃ (21)

Каковы при этом будут оценки коэффициентов?

Здесь уже не будет тех раздельных оценок, которые мы имели в ПФЭ – 2^k

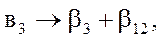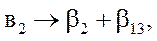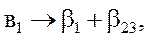Оценки смешаются следующим образом:

где β – математическое ожидание для соответствующих коэффициентов.

Но мы можем считать, что все парные взаимодействия не значимы. Главное, мы нашли средство минимизировать число опытов. Вместо 8 можно поставить 4 опыта и получить те же результаты. При этом матрица планирования не теряет своих оптимальных свойств.

Найденное правило можно сформулировать так: чтобы сократить количество опытов нужно новому фактору присвоить вектор-столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца.

Для того чтобы определить смешанность оценок коэффициентов, удобно пользоваться таким приемом: поставив в матрице x₃ на место x₁x₂, получаем соотношение x₃ = x₁x₂, называемое генерирующим соотношением.

Умножим обе части генерирующего соотношения на x_3:

x₃² =x₁x₂x₃, x₃² = 1, I = x₁x₂x_3..

Полученное выражение называется определяющим контрастом. При помощи этих характеристик определяют смешанность оценок коэффициентов уравнения регрессии. Умножив по очереди определяющий контраст на x₁, x₂, x₃ получим:

x₁ = x₁²x₂x₃ = x₂ x_3, x₂ = x₁x_3, x₃ = x₁x_2..

Следовательно, коэффициенты b_i будут оценивать сумму коэффициентов, т.е. коэффициенты будут менее точными, чем в ПФЭ,

b₁ = b₁ + b₂₃, b₂ = b₂ + b_13, b₃ = b₃ +b₁₂.

Дата добавления: 2014-01-05