Планы первого порядка

Метод крутого восхождения (Бокса- Уилсона)

Этот метод является синтезом лучших черт градиентных методов, метода Гаусса-Зейделя и методов ПФЭ и ДФЭ – как средства получения математической модели процесса. Решение задачи оптимизации данным методом выполняется так, чтобы шаговое движение осуществлялось в направлении наискорейшего возрастания (убывания) параметра оптимизации. Корректировка направления движения (в отличие от градиентных методов) производится не после каждого шага, а по достижению частного экстремума целевой функции. Далее в точках частного экстремума ставится новый факторный эксперимент, составляется новая математическая модель и вновь повторяется крутое восхождение до достижения глобального оптимума. Движение по градиенту начинают из нулевой точки(центра плана).

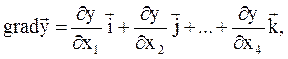Метод крутого восхождения предполагает движение к оптимуму по градиенту.

(26)

где i,j,k-единичные векторы в направлении соответствующих координатных осей.

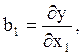
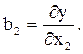(27)

Порядок расчёта.

Исходными данными является математическая модель процесса, полученная любым способом (ПФЭ, ДФЭ и т.д.).

Расчеты проводят в следующем порядке:

а) уравнение регрессии лучше перевести в натуральный вид по формулам кодирования переменных:

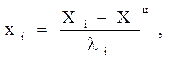
где x _i-кодированное значение переменной x_i;

X_i- натуральное значение переменной x_i;

X_i^Ц-центральный уровень фактора в натуральном виде;

l_i -интервал варьирования фактора x_i в натуральном виде.

Далее все вычисления проводят по уравнению в натуральном виде.

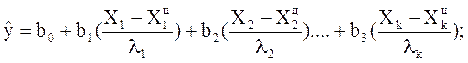
б) вычисляют шаги движения к оптимуму по каждому фактору.

Для этого вычисляют произведения коэффициентов уравнения регрессии в натуральном виде на соответствующие интервалы варьирования

B_i*.l_{I ,}

Затем выбирают из полученных произведений максимальное по модулю,а соответствующий этому произведению фактор принимают за базовый фактор(B_al_a). Для базового фактора следует установить шаг движения, который рекомендуется задавать меньшим или равным интервалу варьирования базового фактоpa

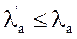Знак шага движения l_a^’ должен совпадать со знаком коэффициента уравнения регрессии, соответствующего базовому фактору (B_a). Величина шагов для других факторов вычисляется пропорционально базовому по формуле:

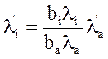
(30)

Знаки шагов движения также должны совпадать со знаками соответствующих коэффициентов уравнения регрессии.

в) вычисляют функцию отклика в центре плана, т. е. при значениях факторов равных центральному уровню факторов, т. к. движение к оптимуму начинают из центра плана.

Далее производят вычисление параметра оптимизации, увеличивая значения факторов на величину соответствующего шага движения, если хотят получить Y_max. В противном случае, если необходимо получить Y_min, значения факторов уменьшают на величину шага движения.

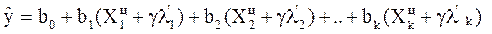
Процедуру повторяют, последовательно увеличивая количество шагов до тех пор, пока не достигнут желаемого значения параметра оптимизации (Y). Каждый из факторов после g шагов будет иметь значение:

Если Y® max X_i=X_i^ц+gl_i`_’

если Y® min. X_i=X_i ^ц-gl_i^`.

Когда закончить расчёт?

При движении по градиенту возможны различные ситуации. Рассмотрим 5 ситуаций, наиболее часто встречающихся на практике.

	x

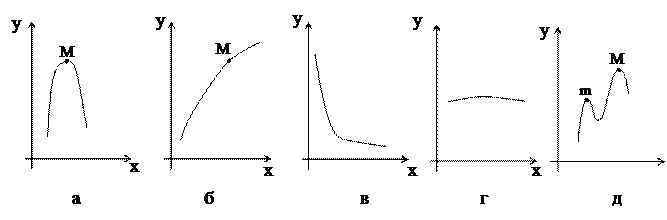
Рисунок 2 – Зависимость параметра оптимизации (у) от фактора (х)

Наиболее благоприятны случаи а, б, д, где движение по градиенту оказалось эффективным.

Движение по градиенту считается эффективным, если его реализация приводит к улучшению значения параметра оптимизации (Y) по сравнению с самым лучшим результатом его в исходной матрице.

а) Расчёт ведут до убывания значения Y, затем возвращаются на шаг назад к Y_max.Это самый идеальный случай, не очень часто встречающийся на практике.

б) Кривая уходит за границы области факторного пространства. В этом случае следует накладывать ограничения либо на Y, либо на X_i. При решении вопроса о наложении ограничений следует руководствоваться технологическими соображениями. Если выход значений X_i за границы области факторного пространства недопустим (взрыв, осмоление продукта), то ограничения накладывают на X_i. Если при движении по градиенту достигнута граница области определения одного или нескольких факторов, дальше двигаться по этому фактору нельзя. Следует зафиксировать значение этого фактора на достигнутом уровне и далее двигаться по остальным факторам до тех пор, пока они тоже не достигнут границ области факторного пространства.

На практике допускают небольшой выход за границы факторного пространства, но надо обязательно проверять полученный результат экспериментально.

Следует помнить, что зависимость Y от X_i полученa только в пределах области факторного пространства, а за его пределами может быть совершенно иная зависимость, т. е. другое уравнение регрессии.

В том случае, когда заранее знают, какой параметр оптимизации хотят получить, ограничения накладывают на (Y). Например, выход продукта 80-90%. Однако и здесь надо следить за значениями X_i и не допускать значительного выхода их за границы области факторного пространства.

в) Случай иллюстрирует неэффективность крутого восхождения. Вместо ожидаемого увеличения параметра оптимизации наблюдается его уменьшение. Здесь либо центр плана расположен в области оптимума, либо есть грубые ошибки в эксперименте. Лучше перейти к планам второго порядка.

г) Все значения Y с увеличением X_i практически одинаковы. Поверхность отклика имеет вид простого гребня. Движение по градиенту неэффективно. Лучше перейти к планам второго порядка.

д) Нарушено требование к поверхности отклика - одноэкстремальность. Здесь следует двигаться по градиенту до достижения локального экстремума в точке (m). Затем, приняв эту точку за центр плана, реализовать ДФЭ, и двигаться по градиенту до достижения глобального оптимума в точке M.

Как влияют на крутое восхождение соотношения численных значений коэффициентов уравнения регрессии?

Если в адекватном уравнении регрессии значим один коэффициент, т.е. многофакторная задача вырождается в однофакторную, то задача оптимизации менее эффективна. Следует выявить причины такого результата, устранить их и получить многофакторную математическую модель.

Коэффициент В₀ на расчет градиента влияния не оказывает.

Качественные факторы фиксируют на одном уровне.

Незначимые факторы стабилизируют на любом уровне(0,+1,1), руководствуясь чисто технологическими или экономическими соображениями.

На практике чаще всего встречаются случаи, когда коэффициенты уравнения различны по значению, но остаются значимыми.

Движение по градиенту наиболее эффективно если уравнение регрессии имеет симметричный вид, т.е. коэффициенты уравнения различаются между собой не более, чем на порядок. На первом этапе планирования эксперимента не всегда удается получить симметричную функцию отклика. Если функция резко асимметрична, то выгоднее вновь поставить эксперимент, изменив интервалы варьирования по факторам, которые более чем на порядок отличаются от других и, получив симметричную функцию, осуществить движение по градиенту.

Почему движение по градиенту начинают из центра плана?

Движение по градиенту начинают из нулевой точки, т.к. функция отклика, вид которой был неизвестен, разлагалась в ряд Тейлора в окрестности нулевой точки. Именно к этой точке и относится оценка градиента.

Достоинства метода: высокая скорость движения к оптимуму, высокая эффективность и точность. Метод эффективен при пологих поверхностях отклика.

Недостатки метода: метод требует наличия математической модели процесса.

5 ЗАДАНИЕ НА РАСЧЕТНУЮ РАБОТУ

Дата добавления: 2014-01-05