Пересечение прямого кругового цилиндра

При пересечении прямого кругового цилиндра вращения секущей плоскостью Р от положения последней могут получиться:

- окружность (рис. 8.7), если плоскость перпендикулярна оси цилиндра i и параллельна основанию, где m₁, m₂ – ее проекции на комплексном чертеже;

- прямоугольник, если плоскость параллельна оси цилиндра i;

- эллипс (рис. 8.8), если плоскость расположена под углом к оси i.

Рис. 8.7.

Покажем комплексный чертеж сечения цилиндра фронтально проецирующей плоскостью Р (Р₁, Р₂). Натуральную величину сечения определяют способом совмещения секущей плоскости Р с плоскостью проекций (рис. 8.8).

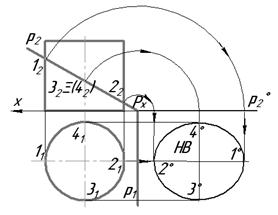
Рис. 8.8.

Полная развертка прямого кругового цилиндра состоит из развертки боковой поверхности и натуральной величины верхнего и нижнего оснований или фигуры сечения.

Развертка боковой поверхности прямого кругового цилиндра представляет собой прямоугольник с высотой h, равной высоте цилиндра, и длиной L = πD, где D – диаметр цилиндра. Для построения на развертке боковой поверхности цилиндра линии среза (рис. 8.9) разбивают окружность основания на n равных частей (в нашем случае на восемь – I…VIII). Затем отмечают эти точки на развертке основания и восстанавливают в них перпендикуляры, на которых откладывают усеченные части соответствующих образующих (точки 1…8), начиная с наименьшей. Соединяя полученные точки плавной кривой, получают развернутое сечение цилиндра в виде синусоиды. Натуральная величина сечения и нижнего основания на рисунке не показаны.

Рис. 8.9.

Для построения на развертке цилиндра произвольной точки А, принадлежащей его боковой поверхности, проводят образующую, на которой располагается точка А, на расстоянии - ℓ_А, измеренное по длине дуги окружности до ближайшей образующей точек разбивки основания на равные части, и на высоте h_А.

Дата добавления: 2014-01-05