Пересечение прямого кругового конуса

При пересечении прямого кругового конуса вращения секущей плоскостью Р от положения последней могут получиться:

- эллипс (рис. 8.10), если плоскость пересекает все образующие конуса вращения;

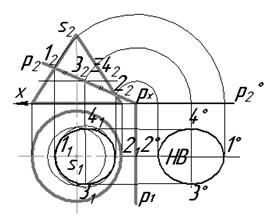
Рис. 8.10.

- окружность (рис. 8.11), если плоскость перпендикулярна оси конуса i и параллельна основанию конуса (частный случай);

- треугольник, если плоскость проходит через вершину конуса (частный случай);

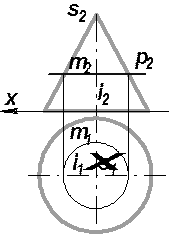
Рис. 8.11.

- гипербола (рис. 8.12), если плоскость параллельна двум образующим конуса - ℓ и (ℓ^/);

- парабола (рис. 8.13),, если плоскостьпараллельна одной образующей конуса - ℓ; парабола вырождается в прямую, если плоскость касается конуса по образующей (частный случай).

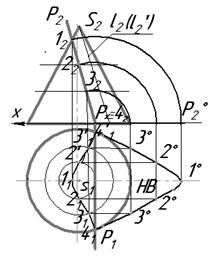
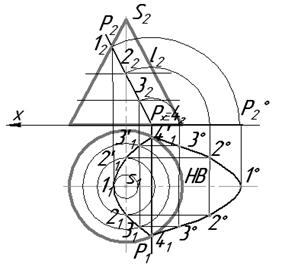
Рис. 8.12. Рис. 8.13.

Полная развертка поверхности прямого кругового конуса состоит из развертки его боковой поверхности и окружности основания (рис. 8.14). Развертка боковой поверхности представляет собой сектор, радиус которого равен длине L образующей конуса, а центральный угол сектора φ = 180⁰D / L (где D – диаметр основания). Очевидно, что длина дуги сектора равна длине окружности πD основания конуса.

Для построения на развертке боковой поверхности конуса линии среза (рис. 8.14) разбивают окружность основания на n равных частей (в нашем случае на восемь – I…VIII) и отмечают эти же точки на развертке. Затем через эти точки проводят образующие (S-I, …, S-VIII) и их горизонтальные и фронтальные проекции на комплексном чертеже (I_1, …, VIII₁; I_2, …., VIII₂). Отмечают фронтальные проекции точек 1…8 пересечения образующих конуса с секущей плоскостью (1₂, …, 8₂); а горизонтальные проекции определяются по линиям проекционной связи на соответствующих образующих (1₁, …., 8₁). На развертке боковой поверхности откладывают усеченные части соответствующих образующих (расстояния от вершины S до точек 1…8), начиная с наименьшей. Истинная величина этих отрезков определяется на комплексном чертеже вращением относительно оси конуса до положения фронтального уровня. При таком положении любая образующая совпадает с очерковой образующей, на которой и берется определяемая длина (S-1, …., S-8). Соединяя полученные точки плавной кривой, получают развернутое сечение конуса.

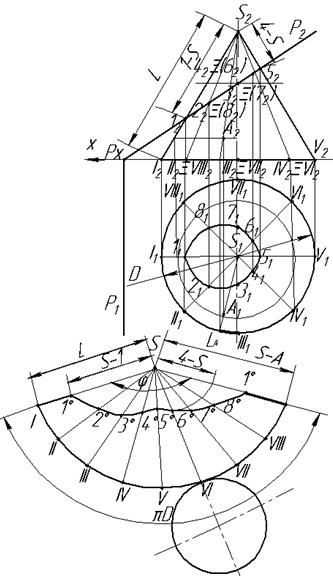
Рис. 8.14.

Для построения на развертке конуса произвольной точки А, принадлежащей его боковой поверхности, сначала проводят образующую, на которой располагается точка А, на расстоянии - ℓ_А, измеренное по длине дуги окружности до ближайшей образующей точек разбивки (II₁) основания на равные части, а затем откладывают натуральную величину расстояния от вершины конуса до точки (S-A). Натуральная величина сечения на рисунке не показана.

Дата добавления: 2014-01-05