Ситуация равновесия в биматричных играх

Мы предполагаем уделить основное внимание случаю, когда у каждого из игроков имеется ровно две стратегии, т. е. случаю т = п = 2. Поэтому нам кажется уместным выписать приведенные выше формулы именно для такого случая.

В 2 ´ 2 биматричной игре платежные матрицы игроков имеют следующий вид

, ,

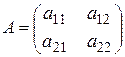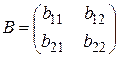вероятности

биматричная игра решение

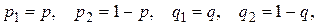
а средние выигрыши вычисляются по формулам

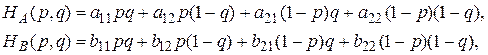
где

,

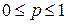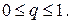
Сформулируем основное определение.

Определение. Будем считать, что пара чисел

, ,

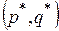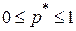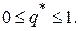
определяет равновесную ситуацию, если для любых р и q, подчиненных условиям 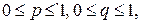одновременно выполнены следующие неравенства

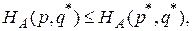
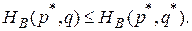(1)

Пояснение. Выписанные неравенства (1) означают следующее: ситуация, определяемая смешанной стратегией (р*, q*), является равновесной, если отклонение от нее одного из игроков при условии, что другой сохраняет свой выбор, приводит к тому, что выигрыш отклонившегося игрока может только уменьшиться. Тем самым, получается, что если равновесная ситуация существует, то отклонение от нее невыгодно самому игроку.

Теорема 1 (Дж. Нэш). Всякая биматричная игра имеет хотя бы одну равновесную ситуацию (точку равновесия) в смешанных стратегиях.

Итак, равновесная ситуация существует. Но как ее найти?

Если некоторая пара чисел (р*, q*) претендует на то, чтобы определять ситуацию равновесия, то для того, чтобы убедиться в обоснованности этих претензий, или, наоборот, доказать их необоснованность, необходимо проверить справедливость неравенств (1) для любого р в пределах от 0 до 1 и для любого q в пределах от 0 до 1. В общем случае число таких проверок бесконечно. И, следовательно, действенный способ определения равновесной ситуации нужно искать где-то в ином месте.

Теорема 2. Выполнение неравенств

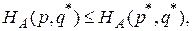
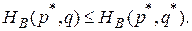(1)

равносильно выполнению неравенств

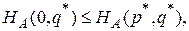
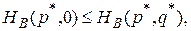
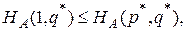
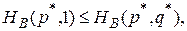(2)

Иными словами, для того, чтобы убедиться в обоснованности претензий пары (р*, q*) на то, чтобы определять равновесную ситуацию, нужно проверить справедливость неравенства

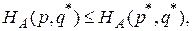
только для двух чистых стратегий игрока А (р = 0 и р = 1) и неравенства

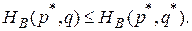
только для двух чистых стратегий игрока В (q = 0 и q= 1).

Четыре неравенства (2) позволяют провести поиск точки равновесия вполне конструктивно.

Запишем средние выигрыши игроков А и В в более удобной форме.

Имеем

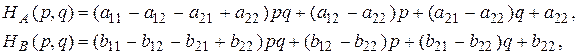
Обратимся к первой из полученных формул.

Полагая в ней сначала р = 1, а потом р = 0, получаем,

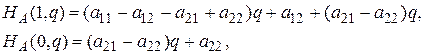
Рассмотрим разности

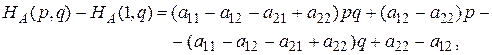
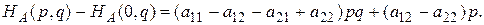
Полагая

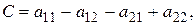
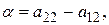
получим для них следующие выражения

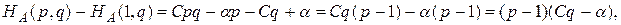
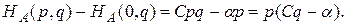
В случае, если пара (р, q) определяет точку равновесия, эти разности неотрицательны

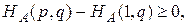
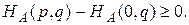
Поэтому окончательно получаем

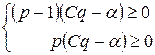
Из формул для функции н_в (р, q) при q = 1 и q = 0 соответственно имеем

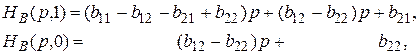
Разност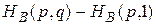и

и

с учетом обозначений

.

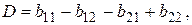
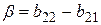приводятся к виду

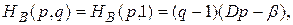
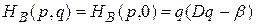
совершенно так же, как соответствующие разности для функции Н_А.

Если пара (р, q) определяет точку равновесия, то эти разности неотрицательны

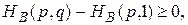
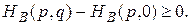
Поэтому

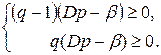
Дата добавления: 2014-01-05