Лекция № 5-6. Бесконечные антагонистические игры

Вывод

Для того, чтобы в биматричной игре

, ,

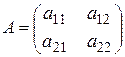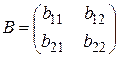пара (р, q) определяла равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств

, ,

, ,

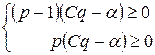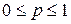где

.

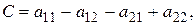
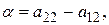
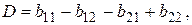
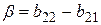Вопросы для самоконтроля:

1. В каком случае возникает биматричная игра, чем она задается?

2. Как можно задать функции выигрыша игроков?

3. Как определяются смешанные стратегии игроков и функции выигрыша игроков?

4. Как определяется ситуация равновесия в биматричной игре?

5. В чем содержательный смысл ситуации равновесия?

6. В каком смысле седловая точка является частным случаем ситуации равновесия?

7. Какая пара стратегий игроков называется оптимальной по Парето?

8. Что означает содержательно оптимальность по Парето?

9. В чем формальное различие между ситуацией равновесия и ситуацией, оптимальной по Парето?

10.Как связаны ситуация равновесия и Парето-оптимальная стратегия в матричных играх?

11. Всегда ли в биматричной игре есть ситуация равновесия?

12.Сформулируйте теорему Брауэра.

13.Всегда ли в биматричной игре есть чистая ситуация равновесия?

14.Являются ли разными ситуации равновесия эквивалентными по значениям функций выигрыша.

15.Что понимается под возможной в игре неустойчивостью ситуации равновесия?

16. Опишите алгоритм поиска ситуации равновесия в биматричных играх размерности 2×2. Что такое вполне смешанные стратегии?

17.Что такое совместная смешанная стратегия? Как могут быть реализованы на практике такие стратегии?

18.Как определяются выигрыши игроков при совместной смешанной стратегии?

19. Как задается в биматричной игре совместная смешанная стратегия?

20. Как определяется в биматричной игре ситуация равновесия в совместных смешанных стратегиях?

21. Какова структура множества ситуаций равновесия в совместных смешанных стратегиях биматричной игры размерности n×m?

22. Какова связь между ситуациями равновесия в смешанных и в совместных смешанных стратегиях?

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.
2. Мазалов В.В. Математическая теория игр и приложения: Учебное пособие. М.: Лань, 2010
3. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.
4. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.
5. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.
2. Волков Ю.И., Волков А.Ю. Теория игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
3. Захаров С.Д. Курс теории игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
4. Данилов В.И. Лекции по теории игр [Электронный ресурс]. КЛ/2002/001. М.: РЭШ, 2002.-192 с.

Цель: изучить особенности решения бесконечных антагонистических игр.

Ключевые слова: бесконечная антагонистическая игра, решение бесконечной антагонистической игры, чистая и смешанная стратегия, седловая точка.

1. Определение бесконечной антагонистической игры.

2. Игры с выпуклыми функциями выигрышей.

Дата добавления: 2014-01-05