
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Игры с выпуклыми функциями выигрышей
|
|
|
|
Игры с выпуклыми непрерывными функциями выигрышей, называемые часто ядром, называются выпуклыми.
Напомним, что выпуклой функцией f действительной переменной х на интервале (а,b) называется такая функция, для которой выполняется неравенство
f(a1 х1 + a2 х2) £ a1 f(х1) + a2 f(х2),
где х1 и х2 любые две точки из интервала (а,b); a1, a2 ³ 0, причём a1 + a2 = 1.
Если для a1 ¹ 0, a2 ¹ 0 всегда имеет место строгое неравенство
f(a1 х1 + a2 х2) < a1 f(х1) + a2 f(х2),
то функция f называется строго выпуклой на (а;b). Геометрически выпуклая функция изображает дугу, график которой расположен ниже стягивающей её хорды (см. рис.)
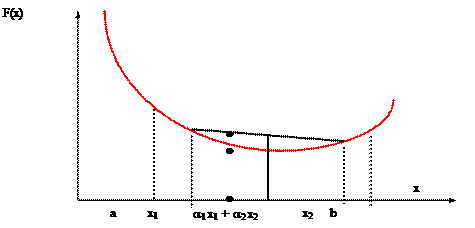
Напомним, также, что непрерывная и строго выпуклая функция f на замкнутом интервале принимает минимальное значение только в одной точке интервала.
Для нахождения решения выпуклой игры можно воспользоваться следующей теоремой.
Теорема 4. Пусть М(х, y) непрерывная функция выигрышей игрока 1, на единичном квадрате и строго выпуклая по y для любого х. Тогда имеется единственная оптимальная чистая стратегия y = yo Î[0;1] для игрока 2, цена игры определяется по формуле
V = 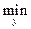
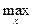 M(x, y),
M(x, y), 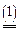
значение yo определяется как решение следующего уравнения
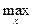 M(x, yo) = V.
M(x, yo) = V. 
Замечание. Если в теореме 4 не предполагать строгую выпуклость функции М(х, y) по y, а просто выпуклость, то теорема остаётся в силе с тем отличием, что у игрока 2 оптимальная чистая стратегия не будет единственной.
Замечание. Выпуклые игры называют часто выпукло-вогнутыми, т.к. игра в них имеет седлообразное ядро, а так как ядро седлообразное, то игра имеет седловую точку в чистых стратегиях.
Таким образом, если М(х, y) непрерывна и выпукла по y, то цена игры определяется по формуле (1), и игрок 2 имеет оптимальную чистую стратегию, определяемую из уравнения (2).
Аналогично и для игрока 1: если функция выигрышей М(х, y) непрерывна по обоим аргументам и строго вогнута по х при любом y, то в этом случае игрок 1 имеет единственную оптимальную стратегию.
Цена игры определяется по формуле
V = 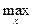
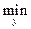 M(x,y),
M(x,y), 
а чистая оптимальная стратегия хo игрока 1 определяется из уравнения
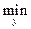 M(xo, y) = V.
M(xo, y) = V. 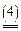
Пример. Пусть на квадрате [0;1] задана функция
М(х, y) =  .
. 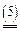
Так как
 для x Î[0; 1], y Î(0;1),
для x Î[0; 1], y Î(0;1),
то М(х, y) строго вогнута по х для любого y Î(0;1). Следовательно, цена игры находится по формуле (3)
V = 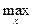
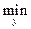
 .
.
Отметим, что при 0 £ х £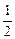 справедливо равенство
справедливо равенство

 =
= 
а при 0,5 < х £ 1

 =
= 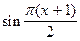
Поэтому
V = max [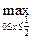

 ;
; 

 ] =
] =
= max [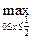
 ;
; 
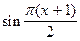 ] =
] =
= max [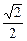 ;
;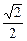 ] =
] = 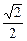 .
.
При этом значение х получается равным хo = 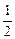 . Это же значение получается из решения уравнения
. Это же значение получается из решения уравнения

 =
= 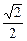 ,
,
т.к. минимум достигается при y = 0, и это уравнение превращается в следующее
 =
= 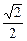 ,
,
откуда следует, что х = 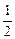 .
.
Заметим, что если в функции выигрышей (5) поменять местами х и y, то она не изменится, а следовательно, эта функция выпукла и по y при всех х Î[0;1]. Поэтому к ней применима та же теория, т.е. у игрока 2 существует оптимальная чистая стратегия yo, определяемая из уравнения (4)

 =
= 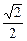
Очевидно, максимум по х достигается при х = 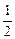 , и последнее уравнение примет вид
, и последнее уравнение примет вид
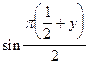 =
= 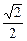 .
.
Решением последнего уравнения будет yo = 0. Следовательно, игрок 2 имеет оптимальную чистую стратегию yo = 0.
Замечание. В приведённом выше примере мы могли определить оптимальную стратегию игрока 1, а игрока 2 - только случайно, в силу удачного вида М(х, y).
Рассмотрим теперь метод определения оптимальных стратегий того игрока, для которого функция выигрышей не обязательно выпукла. Пусть непрерывная функция М(х, y), заданная на единичном квадрате, выпукла по y. Нас будет интересовать вопрос нахождения оптимальных стратегий 1 игрока. Предположим также, что для х Î[0; 1], y Î[0; 1] существует частная производная функции М(х, y) по y, причём в точках y = 0 и y = 1 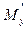 (х, y) =
(х, y) =  понимается как правая и левая производная соответственно. Обозначим через yo одну из оптимальных чистых стратегий игрока 2 (эта стратегия существует в соответствии с теоремой 4).
понимается как правая и левая производная соответственно. Обозначим через yo одну из оптимальных чистых стратегий игрока 2 (эта стратегия существует в соответствии с теоремой 4).
Согласно теореме 2 чистые стратегии х игрока 1 могут входить в его оптимальную стратегию с положительной вероятностью, если для них выполняется равенство
М(х, yo) = V.
Такие чистые стратегии х называются существенными.
Теорема 5. Пусть дана бесконечная антагонистическая игра с непрерывной и дифференцируемой по y на единичном квадрате при любом х функцией выигрышей М(х, y), с оптимальной чистой стратегией yo игрока 2 и ценой игры V, тогда:
1) если yo = 1, то среди оптимальных стратегий игрока 1 имеется существенная чистая стратегия х1, для которой
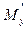 (х1, 1) £ 1;
(х1, 1) £ 1;
2) если yo = 0, то среди оптимальных стратегий игрока 1 имеется существенная чистая стратегия х2, для которой
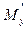 (х2, 0) ³ 0;
(х2, 0) ³ 0;
3) если 0 £ yo £ 1, то среди оптимальных стратегий игрока 1 найдётся такая, которая является смесью двух существенных стратегий х1 и х2. Для этих стратегий
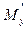 (х1, yo) £ 0,
(х1, yo) £ 0, 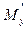 (х2, yo) ³ 0,
(х2, yo) ³ 0,
стратегия х1 употребляется с вероятностью a, стратегия х2 с вероятностью (1 - a), где a находится из уравнения
a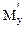 (х1, yo) + (1 - a)
(х1, yo) + (1 - a)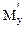 (х2, yo) = 0.
(х2, yo) = 0. 
Пример. Пусть функция выигрышей в бесконечной антагонистической игре задана на единичном квадрате и равна
М(х, y) = (х - y)2 = х2 - 2хy + y2.
Эта функция непрерывна по х и y, и поэтому эта игра имеет решение. Кроме того
 = 2 > 0.
= 2 > 0.
Следовательно, М(х, y) выпукла по y, и поэтому согласно теореме 4 цена игры определяется по формуле (1), игрок 2 имеет чистую оптимальную стратегию yo, определяемую из уравнения (2). Таким образом, имеем
V = 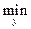
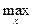 (x - y)2;
(x - y)2;
Для определения 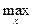 (x2 - 2xy + y2) последовательно найдём
(x2 - 2xy + y2) последовательно найдём
 = 2x - 2y:= 0 Þ x = y
= 2x - 2y:= 0 Þ x = y
 = 2 > 0 Þ при x = y функция M имеет минимум для любого y.
= 2 > 0 Þ при x = y функция M имеет минимум для любого y.
Þ максимум достигается в одной из крайних точек x = 0 и (или) x = 1
M(0; y) = y2
M(1; y) = 1 - 2y + y2 = (y - 1)2
V= max {y2; (1 - y)2}
max {y2; (1 - y)2}
Данный  max {...} достигается в том случае, если y2 = (1 - y)2, т.е. y =
max {...} достигается в том случае, если y2 = (1 - y)2, т.е. y = 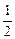 .
.
Следовательно V =  при yo =
при yo = 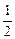 .
.
Определим теперь оптимальные стратегии для игрока 1. Поскольку yo = 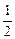 , то 0 < yo < 1. Согласно теореме 5 рассмотрим третий случай.
, то 0 < yo < 1. Согласно теореме 5 рассмотрим третий случай.
Определим х из уравнения
М(х, yo) = V,
то есть
(х -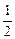 )2 =
)2 =  .
.
Решая последнее уравнение, получим х1 = 0, х2 = 1. Теперь необходимо определить величину a вероятность применения чистой стратегии х1 = 0. С этой целью используем уравнение (*).
a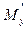 (0,
(0,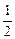 ) + (1 - a)
) + (1 - a)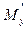 (1,
(1,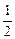 ) = 0.
) = 0.
Нетрудно найти

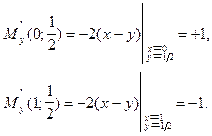
Тогда уравнение для a примет вид:
a - (1 - a) = 0,
откуда a =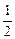 . Следовательно, стратегия игрока 1
. Следовательно, стратегия игрока 1
F(х) = 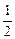 Jo(х) +
Jo(х) + 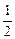 J1(х),
J1(х),
а игрока 2
Q(y) = 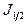 (y).
(y).
Здесь через  (x) обозначена ступенчатая функция
(x) обозначена ступенчатая функция
 (x) =
(x) = 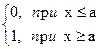 .
.
Вопросы для самоконтроля:
1. Как называется задача принятия решения, в которых на систему воздействует не одна, а несколько управляющих подсистем, каждая из которых имеет свои цели и возможности действий?
2. Математическая модель какого конфликта называется антагонистической игрой?
3. Чем определяется состояние такой системы? Антагонистическую игру естественно задать системой Г= (Х, Y, F).
4. Какая игра называется антагонистической и какими объектами ее задают?
5. В чем содержательное различие между управляющей подсистемой и средой?
6. Как называется антагонистическая игра, если Х и Y конечны?
7. Как определяются нижняя цена игры и верхняя цена игры? Как определяется цена игры?
8. Каково соотношение между максимином и минимаксом?
9. Что такое седловая точка? К чему приводит одностороннее отступление игрока от седловой точки?
10. Чему равно значение функции выигрыша в седловой точке?
11.Сформулируйте теорему о взаимозаменяемости и эквивалентности cедловых точек.
12. Сформируйте достаточное условие существования седловой точки.
13. При каких условиях в выпуклой игре у игрока есть единственная оптимальная стратегия?
Список литературы
Основная:
- Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.
- Мазалов В.В. Математическая теория игр и приложения: Учебное пособие. М.: Лань, 2010
- Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.
- Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.
- Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.
Дополнительная:
- Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.
- Волков Ю.И., Волков А.Ю. Теория игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
- Захаров С.Д. Курс теории игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
- Данилов В.И. Лекции по теории игр [Электронный ресурс]. КЛ/2002/001. М.: РЭШ, 2002.-192 с.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 1499; Нарушение авторских прав?; Мы поможем в написании вашей работы!