Пример. Министерство желает построить один из двух объектов на территории города

Министерство желает построить один из двух объектов на территории города. Городские власти могут принять предложения министерства или отказать. Министерство  игрок 1  имеет две стратегии: строить объект 1, строить объект 2. Город  игрок 2  имеет две стратегии: принять предложение министерства или отказать. Свои действия (стратегии) они применяют независимо друг от друга, и результаты определяются прибылью (выигрышем) согласно следующим матрицам:

A = , B =

(например: если игроки применяют свои первые стратегии, министерство решает строить 1 объект, а городские власти разрешают его постройку, тогда город получает выигрыш 5 млн, а министерство теряет 10 млн, и т.д.)

Решение. Для этой игры имеем:

a1 = a11 - a12 - a21 + a22 = -10 - 2 - 1 - 1 = -14 < 0,

a2 = a22 - a12 = -1 - 2 = -3,

.

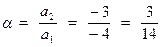Так как a1 < 0, то множество решений K имеет следующий вид:

(0, y) при ;

(x, 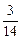) при 0 £ x £ 1;

(1, y) при 0 £ y £ .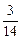

Для 2 игрока имеем:

b1 = b11 - b12 - b21 + b22 = 5 + 2 + 1 + 1 = 9 > 0,

b2 = b22 - b21 = 1 + 1 = 2,

.

y

Так как b1 > 0, то множество решений L L

имеет следующий вид:

K

(x; 0), при 0 £ x £;

(; y), при 0 £ y £ 1; 0 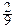1 x

(x; 1), при £ x £ 1.

Точка пересечения множеств L и K есть точка C с координатами x = ; y = 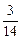и является соответственно приемлемыми стратегиями министерства и города.

При этом выигрыш соответственно равен

E1(A,x,y) = (x, 1-x)=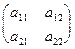

= =

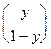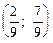
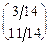E2(A,x,y) = (x, 1-x)=

Замечание. Если решить эту игру как матричные игры двух игроков с нулевой суммой, то для игры с матрицей A оптимальные смешанные для 1 игрока и цена игры получаются из решения уравнений

откуда вероятность применения игроком 1 первой стратегии равна 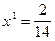, цена игры  , что совпадает с E1, вероятность применения игроком 2 первой стратегии 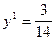; для игры с матрицей B оптимальные смешанные стратегии и цена игры для игрока 2 определяются из системы:

Следовательно, вероятность применения игроком 2 своей стратегии , а игроком 1, цена игры , что совпадает с E2.

Таким образом, если каждый из игроков будет применять свои стратегии в этой игре, исходя только из матриц своих выигрышей, то их оптимальные средние выигрыши совпадают с их выигрышами при ситуации равновесия.

Вопросы для самоконтроля:

1. Дайте определение бескоалиционной игры?

2. Какие виды бескоалиционных игр вы знаете?

3. В чем заключается основная идея решения таких игр?

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.
2. Мазалов В.В. Математическая теория игр и приложения: Учебное пособие. М.: Лань, 2010
3. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.
4. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.
5. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.
2. Волков Ю.И., Волков А.Ю. Теория игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
3. Захаров С.Д. Курс теории игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
4. Данилов В.И. Лекции по теории игр [Электронный ресурс]. КЛ/2002/001. М.: РЭШ, 2002.-192 с.

Дата добавления: 2014-01-05