Критерий ожидаемого значения

Лекция № 10.Теория принятия решений в условиях риска.

Цель: изучить особенности основные принципы принятия решений.

Ключевые слова: критерии принятия решений.

1. Критерий ожидаемого значения.

2. Критерий: ожидаемое значение - дисперсия.

3. Критерий предельного уровня.

Использование критерия ожидаемого значения обусловлено стремлением максимизировать ожидаемую прибыль (или минимизировать ожидаемые затраты). Использование ожидаемых величин предполагает возможность многократного решения одной и той же задачи, пока не будут получены достаточно точные расчётные формулы. Математически это выглядит так: пусть Х случайная величина с математическим ожиданием MX и дисперсией DX. Если x1,x2,...,xn  значения случайной величины (с.в.) X, то среднее арифметическое их (выборочное среднее) значений 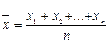имеет дисперсию 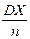. Таким образом, когда n ® ¥

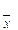® 0 и ® MX.

Другими словами при достаточно большом объёме выборки разница между средним арифметическим и математическим ожиданием стремится к нулю (так называемая предельная теорема теории вероятности). Следовательно, использование критерия ожидаемое значение справедливо только в случае, когда одно и тоже решение приходится применять достаточно большое число раз. Верно и обратное: ориентация на ожидания будет приводить к неверным результатам, для решений, которые приходится принимать небольшое число раз.

Пример 1. Требуется принять решение о том, когда необходимо проводить профилактический ремонт ПЭВМ, чтобы минимизировать потери из-за неисправности. В случае если ремонт будет производится слишком часто, затраты на обслуживание будут большими при малых потерях из-за случайных поломок.

Так как невозможно предсказать заранее, когда возникнет неисправность, необходимо найти вероятность того, что ПЭВМ выйдет из строя в период времени t. В этом и состоит элемент риска.

Математически это выглядит так: ПЭВМ ремонтируется индивидуально, если она остановилась из-за поломки. Через T интервалов времени выполняется профилактический ремонт всех n ПЭВМ. Необходимо определить оптимальное значение Т, при котором минимизируются общие затраты на ремонт неисправных ПЭВМ и проведение профилактического ремонта в расчёте на один интервал времени.

Пусть рt  вероятность выхода из строя одной ПЭВМ в момент t, а nt  случайная величина, равная числу всех вышедших из строя ПЭВМ в тот же момент. Пусть далее С1  затраты на ремонт неисправной ПЭВМ и С2  затраты на профилактический ремонт одной машины.

Применение критерия ожидаемого значения в данном случае оправдано, если ПЭВМ работают в течение большого периода времени. При этом ожидаемые затраты на один интервал составят

ОЗ = ,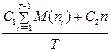

где M(nt)  математическое ожидание числа вышедших из строя ПЭВМ в момент t. Так как nt имеет биномиальное распределение с параметрами (n, pt), то M(nt) = npt. Таким образом

ОЗ =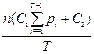

Необходимые условия оптимальности T* имеют вид:

ОЗ (T*-1) ³ ОЗ (T*),

ОЗ (T*+1) ³ ОЗ (T*).

Следовательно, начиная с малого значения T, вычисляют ОЗ(T), пока не будут удовлетворены необходимые условия оптимальности.

Пусть С1 = 100; С2 = 10; n = 50. Значения pt имеют вид:

T	рt		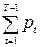ОЗ(Т)
	0.05
	0.07	0.05
	0.10	0.12	366.7
	0.13	0.22
	0.18	0.35

T*® 3, ОЗ(Т*) ® 366.7

Следовательно профилактический ремонт необходимо делать через T*=3 интервала времени.

2. Критерий: ожидаемое значение-дисперсия.

Критерий ожидаемого значения можно модифицировать так, что его можно будет применить и для редко повторяющихся ситуаций.

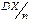Если х  с. в. с дисперсией DX, то среднее арифметическое имеет дисперсию , где n  число слогаемых в . Следовательно, если DX уменьшается, и вероятность того, что 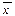близко к MX, увеличивается. Следовательно, целесообразно ввести критерий, в котором максимизация ожидаемого значения прибыли сочетается с минимизацией её дисперсии.

Пример 2. Применим критерий ожидаемое значение  дисперсия для примера 1. Для этого необходимо найти дисперсию затрат за один интервал времени, т.е. дисперсию

зТ =

Т.к. nt, t =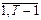  с.в., то зТ также с.в. С.в. nt имеет биномиальное распределение с M(nt) = npt и D(nt) = npt(1pt). Следовательно,

D(зТ) = D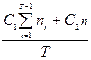 = D() =

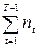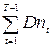= = = n  ,

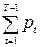
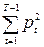где С2n = const.

Из примера 1 следует, что

М(зТ) = М(з(Т)).

Следовательно искомым критерием будет минимум выражения

М(з(Т)) + к D(зТ).

Замечание. Константу к можно рассматривать как уровень не склонности к риску, т.к. к определяет степень возможности дисперсии Д(зТ) по отношению к математическому ожиданию. Например, если предприниматель, особенно остро реагирует на большие отрицательные отклонения прибыли вниз от М(з(Т)), то он может выбрать к много больше 1. Это придаёт больший вес дисперсии и приводит к решению, уменьшающему вероятность больших потерь прибыли.

При к =1 получаем задачу

По данным из примера 1 можно составить следующую таблицу

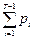
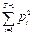
Т	pt	pt2			М(з(Т))+D(з(Т))
	0.05	0.0025			500.00
	0.07	0.0049	0.05	0.0025	6312.50
	0.10	0.0100	0.12	0.0074	6622.22
	0.13	0.0169	0.22	0.0174	6731.25
	0.18	0.0324	0.35	0.0343	6764.00

Из таблицы видно, что профилактический ремонт необходимо делать в течение каждого интервала Т*=1.

Дата добавления: 2014-01-05