Критерий предельного уровня

Критерий предельного уровня не дает оптимального решения, максимизирующего, например, прибыль или минимизирующего затраты. Скорее он соответствует определению приемлемого способа действий.

Пример 3. Предположим, что величина спроса x в единицу времени (интенсивность спроса) на некоторый товар задаётся непрерывной функцией распределения f(x). Если запасы в начальный момент невелики, в дальнейшем возможен дефицит товара. В противном случае к концу рассматриваемого периода запасы нереализованного товара могут оказаться очень большими. В обоих случаях возможны потери.

Т.к. определить потери от дефицита очень трудно, ЛПР может установить необходимый уровень запасов таким образом, чтобы величина ожидаемого дефицита не превышала А1 единиц, а величина ожидаемых излишков не превышала А2 единиц. Иными словами, пусть I  искомый уровень запасов. Тогда

ожидаемый дефицит = ,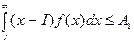

ожидаемые излишки =.

При произвольном выборе А1 и А2 указанные условия могут оказаться противоречивыми. В этом случае необходимо ослабить одно из ограничений, чтобы обеспечить допустимость.

Пусть, например,

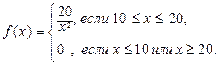
Тогда

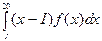= = 20(ln + 1)

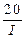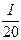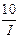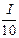= = 20(ln + 1)

Применение критерия предельного уровня приводит к неравенствам

ln I 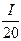 ³ ln 20 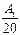  1 = 1.996 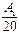

ln I 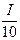 ³ ln 10 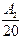  1 = 1.302 

Предельные значения А1 и А2 должны быть выбраны так, что бы оба неравенства выполнялись хотя бы для одного значения I.

Например, если А1 = 2 и А2 = 4, неравенства принимают вид

ln I 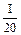 ³ 1.896

ln I 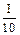 ³ 1.102

Значение I должно находиться между 10 и 20, т.к. именно в этих пределах изменяется спрос. Из таблицы видно, что оба условия выполняются для I, из интервала (13,17)

I
ln I 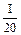	1.8	1.84	1.88	1.91	1.94	1.96	1.97	1.98	1.99	1.99	1.99
ln I 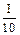	1.3	1.29	1.28	1.26	1.24	1.21	1.17	1.13	1.09	1.04	0.99

Любое из этих значений удовлетворяет условиям задачи.

Вопросы для самоконтроля:

1.Как задается вероятностная мера на множестве состояний природы, если множество конечно?

2.Что такое априорное распределение вероятностей на множестве состояний природы.

3.В каких случаях говорят, что принятие решения происходит в условиях риска?

4.Как определяется критерий математического ожидания?

5.Что такое байесовская стратегия, байесовский подход?

Список литературы

Основная:

1. Оуэн Г. Теория игр. Учебное пособие. Санкт-Петербург: ЛКИ, 2008 – 229 с.
2. Мазалов В.В. Математическая теория игр и приложения: Учебное пособие. М.: Лань, 2010
3. Губко М.В., Новиков Д.А Теория игр в управлении организационными процессами [Электронный ресурс]: Учебное пособие. М.: Наука, 2005 – 138 с.
4. Даниловцева Е.Р., Теория игр: основные понятия: текст лекций [Электронный ресурс]. Санкт-Петербург: СПбГУАП, 2003 – 36 с.
5. Коковин С.Г., Лекции по теории игр [Электронный ресурс]. Новосибирск: Типография НГУ, 2010 г. – 91 с.

Дополнительная:

1. Самаров К.Л. Элементы теории игр [Электронный ресурс]. Учебное пособие. Новосибирск: Типография НГУ, 2010 г. – 91 с.
2. Волков Ю.И., Волков А.Ю. Теория игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
3. Захаров С.Д. Курс теории игр [Электронный ресурс]. Тюмень, ТГИМЭУП, 2002.
4. Данилов В.И. Лекции по теории игр [Электронный ресурс]. КЛ/2002/001. М.: РЭШ, 2002.-192 с.

Лекция № 11-12. Теория принятия решений в условиях неопределённости.

Цель: изучить особенности основные принципы принятия решений в условиях неопределённости.

Ключевые слова: критерии принятия решений в условиях неопределённости.

Вопросы:

1. Постановка задачи;

2. Классические критерии принятия решений.

3. Производные критерии принятия решений.

Дата добавления: 2014-01-05