Фазификатор

Рассмотрим подробнее первый этап процедуры нечеткого вывода.

Фазификатор преобразует N-мерный входной вектор х = [ x₁, x₂, …, x_N ] в нечеткое множество А, характеризуемое функцией принадлежности 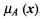с четкими переменными. Несмотря на то, что нечеткие системы могут иметь функции принадлежности произвольной структуры, с практической точки зрения наибольшей популярностью пользуются функции гауссовского типа, а также треугольные и трапецеидальные функции.

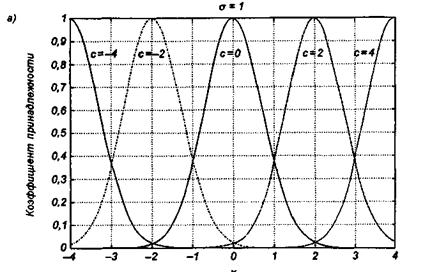
Рис. 6.5 Иллюстрация влияния параметров гауссовской функции на ее форму:

а) влияние размещения центра с при σ = 1;

б) влияние значения σ при постоянном значении с = 1

Общая форма гауссовой функции для переменной х с центром с и вариацией σ для множества F имеет вид:

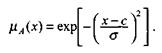(6.7)

На рис. 6.5. представлена форма типовых гауссовских функций при различ­ных параметрах с и σ, причем на рис. 6.5а показано влияние размещения центра с при неизменном значении σ, а на рис. 6.5б - влияние значения σ при фиксиро­ванном положении с. Параметр с обозначает центр нечеткого множества, а его из­менение соответствует смещению функции принадлежности по горизонтальной оси. Праметр σ, иногда называемый коэффициентом широты, отвечает за форму функции. Чем меньше его значение, тем больше крутизна функции. Следует отме­тить, что при соответствующем смещении центра гауссовская функция может реализовать и сигмоидальную функцию (чаще всего при смещении вправо с с =4).

Помимо гауссовской функции принадлежности, на практике часто приме­няется симметричная треугольная функция, которую можно записать в виде

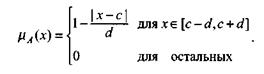(6.8)

Интерпретация центральной точки с и ширины d для треугольной функции представлена на рис.6.6.

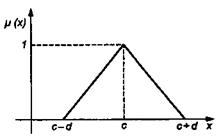
Рис. 6.6 Треугольная форма функции

Эта функция тоже нормирована и принимает единичное значение в центральной точке с.

Обобщением треугольной функции является трапецеидальная функция принадлежности, форма и обозначения кото­рой показаны на рис. 6.7.

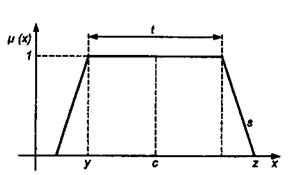
Рис. 6.7 Трапецеидальная форма функции принадлежности

Если определить, 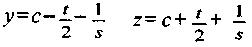, где s обозначает угол наклона, то трапецеидальная функция описывается зависимостью

(6.9)

Выбор значения t = 0 редуцирует трапецеидальную функцию до треугольной формы.

Дата добавления: 2014-01-05