Основные схемы логически правильных рассуждений

Языки логики высказываний содержат правила преобразования логических формул. Эти правила реализуют общелогические законы и тем самым обеспечивают логически правильные рассуждения.

Рассуждение (умозаключение) - процесс получения новых знаний, выраженных высказываниями, из других знаний, также выраженных высказываниями. Исходные высказывания называются посылками (гипотезами, условиями), а получаемые высказывания - заключением (следствием).

Перечислим наиболее употребляемые схем логически правильных рассуждений:

1. Правило заключения - утверждающий модус: «Если из высказывания А следует высказывание В и справедливо (истинно) высказывание А, то справедливо В».

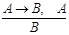
2. Правило отрицания - отрицательный модус: «Если из Аследует В, но высказывание Вневерно, то неверно А.

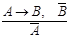
3. Правила утверждения-отрицания: «Если справедливо или высказывание А, или высказывание В (в разделительном смысле) и истинно одно из них, то другое ложно.

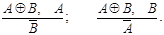
4. Правила отрицания-утверждения:

4.1. «Если истинно или А, или В (в разделительном смысле) и неверно одно из них, то истинно другое».

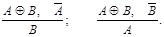
4.2. «Если истинно А или В (в неразделительном смысле) и неверно одно из них, то истинно другое»:

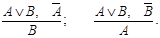
5. Правило транзитивности: «Если из А следует В, а из В следует С, то из Аследует С».

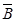6. Закон противоречия: «Если из А следует В и, то неверно А»:

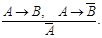
7. Правило контрапозиции: «Если из А следует В, то из того, что неверно В, следует, что неверно А.

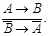
8. Правило сложной контрапозиции: «Если из А и В следует С, то из А и следует неС следует неВ.

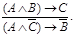
9. Правило сечения: «Если из А следует В, а из В и С следует D то из А и С следует D».

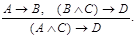
10. Правило импортации (объединения посылок):

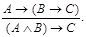
11. Правило экспортации (разъединения посылок):

12. Правила дилемм:

Примечание. Для построения логических формул, отражающих указанные выше логически правильные рассуждения, следует все посылки соединить связкой «И» (&), и полученную, таким образом обобщенную посылку связкой «если то...» (→). Например, правило заключения должно быть представлено логической формулой:

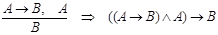
Примерами рассуждений, не являющихся правильными, могут служить:

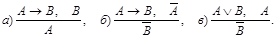
Для того чтобы проверить, является ли данное умозаключение логически правильным, следует восстановить схему рассуждения и определить, относится ли она к схемам логически правильных рассуждений.

Пример 8.

К какой схеме относятся рассуждение: «Если рабочий отсутствовал на работе, он не выполнил задания. Он не выполнил задания. Следовательно, он отсутствовал на работе».

Обозначим каждое из простых высказываний: А - отсутствовал на работе; В – не выполнил задания. Он не выполнил задания (В). «Если рабочий А он В. Он В следовательно, он А». Схема данного рассуждения относится к схеме (а) неправильных рассуждений.

Пример 9.

К какой схеме относятся рассуждение: «Этот человек студент или предприниматель. Он студент. Следовательно, не предприниматель».

Обозначим каждое из простых высказываний: А – студент; В – преподаватель. Этот человек А или В. Он А. Следовательно, не В». Учитывая то, что в первом предложении союз «или» использован в неразделительном смысле. Схема соответствует схеме (в) неправильных рассуждений.

Пример 10.

К какой схеме относятся рассуждение: «Этот человек постоянно живет в Белгороде или Москве. Он живет в Белгороде. Следовательно, он не живет в Москве».

Обозначим каждое из простых высказываний: «Этот человек постоянно живет в Белгороде (А) или Москве (В). Он не живет в Белгороде (неА). Следовательно, он живет в Москве(В)». Рассуждение правильное.

Дата добавления: 2014-01-05