Тема 2.3. Полнота и замкнутость

Резюме по теме

Вопросы для повторения

1.Что называется булевой алгеброй?

2.Является ли базис функций импликация, эквивалентность и отрицание булевой алгеброй?

3.Назовите этапы приведения логической формулы к СДНФ?

4.Каким образом осуществляется замена переменной формулой?

5.Как доказывается эквивалентность формул?

Рассмотрена алгебра логики. Приведены логические функции, которые являются базисом булевой алгебры. Показам способ перехода от любой логической функции к базису булевой алгебры (приведение к СДНФ). Показаны эквивалентные преобразования, используемые при работе по упрощению логических функций.

Цель: изучить функционально полные системы.

Задачи:

1. Рассмотреть функционально полные системы.

2. Рассмотреть алгебру Жегалкина и линейные функции.

3. Ознакомиться с замкнутыми классами и монотонными функциями.

4. Рассмотреть теоремы о функциональной полноте.

Ранее нами рассматривались два способа задания логических функций – табличный и с помощью формул. Таблица задаёт функцию непосредственно как соответствие между двоичными наборами и значениями функции на этих наборах. Этот способ универсален, то есть, пригоден для любых функций, однако слишком громоздок. Формула – гораздо более компактный способ задания функции, но она задаёт функцию через другие функции. Поэтому для любой системы функций 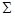возникает естественный вопрос: всякая ли логическая функция представима формулой в этой системе. В предыдущей лекции был получен положительный ответ для системы . В данной лекции будет показано, как решать этот вопрос для произвольной системы .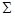

Дата добавления: 2014-01-05