Сочетания

Неупорядоченные выборки объемом m из n элементов (m < n) называются сочетаниями. Их число обозначается .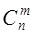

Теорема 5.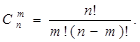

Доказательство. Очевидно, 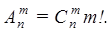Действительно, объект A – неупорядоченная выборка из n элементов по m, их число 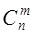. После того, как эти m элементов отобраны, их можно упорядочить m! способами (в роли объекта B выступает “порядок“ в выборке). Совместный выбор “ A и B “ – упорядоченная выборка.

Пример 5.

Группа из 15 человек выиграла 3 одинаковых книги. Сколькими способами можно распределить эти книги?

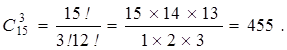
Рассмотрим сочетания, которые не являются подмножествами.

Пусть имеется n типов элементов, каждый тип содержит не менее m одинаковых элементов. Неупорядоченная выборка объемом m из имеющихся элементов (их число ³ m ´ n) называется сочетанием с повторением. Число сочетаний с повторениями обозначается 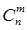(n).

Теорема 6. 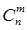(n) = .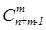

Доказательство. Пусть в выборку вошло m ₁ элементов первого типа, m ₂ элементов второго типа,... m _n – n -го типа. Причем каждое 0 £ m _i £ m и m ₁+ m ₂+...+ m_n = = m. Сопоставим этой выборке вектор следующего вида: 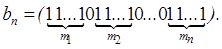Очевидно, между множеством неупорядоченных выборок с повторениями и множеством векторов { b_n } существует биекция (докажите это!). Следовательно, 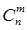(n) равно числу векторов b_n. “ Длина вектора” b_n равна числу 0 и 1, или m + + n– 1. Число векторов равно числу способов, которыми m единиц можно поставить на m + n - 1 мест, а это будет .

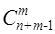Дата добавления: 2014-01-05