Основные понятия. Графические представления в узком смысле - это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов

Графические представления в узком смысле - это описание исследуемой системы, процесса, явления средствами теории графов в виде совокупности двух классов объектов: вершин и соединяющих их линий - ребер или дуг.

Графы и их составляющие характеризуются определенными свойствами и набором допустимых преобразований (операций) над ними.

Графом G называется совокупность двух множеств: вершин V и ребер Е, между элементами которых определено отношение инцидентности.

Отношение инцидентности – когда каждое ребро 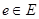инцидентно ровно двум вершинам 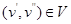, которые оно соединяет. При этом вершина v' (v") и ребро е называются инцидентными друг другу, а вершины v' и v", являющиеся для ребра е концевыми точками, называются смежными. Часто вместо 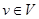и 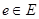пишут соответственно , .

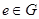Направленное ребро (ориентированное ребро) – ребро, соединяющее две вершины, которое имеет направление от одной вершины к другой и изображается стрелкой, направленной от вершины, называемой началом, к вершине, именуемой концом.

Граф, содержащий направленные ребра (дуги) с началом v' и концом v", называется ориентированным графом (орграфом), а ненаправленные – неориентированным графом (н-графом).

Ребра, инцидентные одной и той же паре вершин, называются параллельными ребрами, или кратными ребрами.

Граф, содержащий кратные ребра, называется мультиграфом.

Ребро, концевые вершины которого совпадают, называется петлей.

Граф называется конечным графом, если множество его элементов (вершин и ребер) конечно, и пустым графом, если его множество вершин V (а значит и ребер Е) пусто.

Граф без петель и кратных ребер называется полным графом, если каждая пара вершин соединена ребром.

Дополнением графа G называется граф , имеющий те же вершины, что и граф G, и содержащий только те ребра, которые нужно добавить к графу G, чтобы получить полный граф.

Каждому неориентированному графу канонически соответствует ориентированный граф с тем же множеством вершин, в котором каждое ребро заменено двумя ориентированными ребрами, инцидентными тем же вершинам и имеющими противоположные направления.

Локальной степенью вершины (или просто степенью) 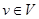н-графа G называется количество ребер p(v), инцидентных вершине v.

В н-графе сумма степеней всех вершин равна удвоенному числу ребер т графа, т.е. четна (предполагается, что в графе с петлями петля дает вклад 2 в степень вершины):

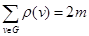
отсюда следует, что в н-графе число вершин нечетной степени четно.

Для вершин орграфа определяются две локальные степени:

• ^_ число ребер с началом в вершине v, или количество выходящих из v ребер;

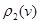• - количество входящих в v ребер, для которых эта вершина является концом.

Петля дает вклад 1 в обе эти степени.

В орграфе суммы степеней всех вершин и 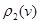равны количеству ребер т этого графа, а значит, и равны между собой:

Графы G₁ и G₂ равны, т.е. G₁ = G₂, если их множества вершин и ребер (выраженных через пары инцидентных им вершин) совпадают: V₁ = V₂ и Е₁=Е₂. Графы G₁ и G₂ на рис. 4.2 равны.

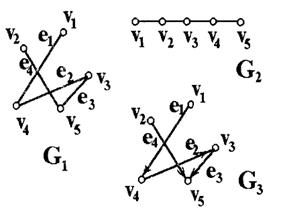
Рис. 4.2. Изображение графов

Граф G считается полностью заданным в строгом смысле, если нумерация его вершин и ребер зафиксирована. Графы, отличающиеся только нумерацией вершин и ребер, называются изоморфными графами.

Пример 1.

Задать граф G₁, представленный на рис. 2 через множества вершин V₁и ребер Е₁

Граф G₁может быть полностью определен:

• двумя множествами поименованных вершин V_l={v₁, v₂, v₃, v₄, v₅} и поименованных ребер Е₁= {e₁,е₂,e₃,е₄} (в строгом смысле требуется установление отношения инцидентности ребер соответствующим вершинам);

• множеством ребер, каждое из которых представлено парой своих концевых вершин: Е= {(v₁, v₄), (v₄, v₃), (v₃, v₅), (v₅,v₂)}. Порядок указания вершин при описании ребра здесь безразличен, так как все ребра в графе G₁ неориентированные.

Дата добавления: 2014-01-05