Пример 2. Способы задания графов

Способы задания графов

В общем виде задать граф - значит описать множества его вершин и ребер, а также отношение инцидентности. Для описания вершин и ребер достаточно их занумеровать. Пусть v₁,v₂,..., v_n - вершины графа G; е₁,е₂,...,е_т - ребра. Отношение инцидентности задается:

• матрицей инцидентности размера тхп: по вертикали и горизонтали указываются вершины и ребра соответственно, а на пересечении i -й вершины и j -го ребра в случае неориентированного графа проставляется 1, если они инцидентны, и 0 - в противном случае, т.е.

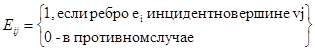
а в случае орграфа: -1, если вершина является началом ребра, 1 - если вершина является концом ребра, и 0 - если вершина и ребро не инцидентны; если некоторая вершина является для ребра и началом, и концом (т.е. ребро - петля), проставляется любое другое число, например 2,

• списком ребер графа, представленным двумя столбцами: в левом перечисляются все ребра , а в правом инцидентные ему вершины v_i,v_j, для н-графа порядок вершин в строке произволен, для орграфа первым стоит номер начала ребра;

• матрицей смежности 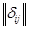| - квадратной матрицей размера п х п: по вертикали и горизонтали перечисляются все вершины , а на пересечении k-й и l-й вершин в случае н-графа проставляется число, равное числу ребер, соединяющих эти вершины; для орграфа 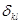равно числу ребер с началом в к-й вершине и концом в l-й.

Если два графа равны, то их матрицы совпадают. Если в графе поменять нумерацию вершин, матрицы (и список ребер) в общем случае изменяются, т.е. вид матриц и списка ребер зависит от нумерации вершин и ребер графа. Граф считается полностью заданным, если нумерация его вершин зафиксирована. Графы, отличающиеся только нумерацией вершин, являются изоморфными.

Задать матрицами инцидентности и смежности, а также списком ребер графы ,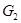(рис. 4.3).

Рис. 4.3. Н-граф G₁ и орграф G₂

Матрицы инцидентности графов и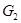приведены в табл. 1. В матрице инцидентности в каждом столбце только два элемента, отличных от 0 (или один, если ребро - петля).

Таблица 1. Матрица инцидентности графов и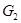

a

b

c

d

e

f

g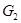

a

b

c

d

e

f

g

-1

-1

-1

-1

-1

-1

Список ребер орграфа 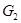приведен в табл. 2 для н–графа он аналогичен, однако последовательность указания вершин здесь безразлична. Матрицы смежности графов ,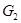даны в табл.3.

Таблица 3.

Таблица 2.

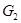
Ребро

Вершины

a

b

c

d

e

f

g

Дата добавления: 2014-01-05