Нормальный закон распределения

Нормальное распределение времени до отказа или распределение Гаусса является наиболее общим законом распределения. Согласно теории больших чисел любое распределение всегда подчиняется нормальному закону в том случае, когда на объект оказывают влияние многие примерно однозначные факторы. Таким образом, нормальное распределение охватывает весь жизненный цикл объекта, а не только его отдельные этапы. Для рассмотренного выше экспоненциального закона распределения характерным являлся этап нормальной работы.

Нормальный закон распределения является двухпараметрическим – имеет два параметра, при помощи которых можно описать изменение всех остальных интересующих нас величин. Этими параметрами являются математическое ожидание m и среднее квадратическое отклонение σ времени безотказной работы элемента.

Математическая запись функции плотности вероятности безотказной работы при нормальном распределении имеет вид:

_{2 2}

f(t) = 1 / (σ· 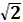π)·е^{-(t – m) / (2 σ)}, - ∞ ≤ t ≤ + ∞.

Этому выражению соответствует график плотности вероятности безотказной работы, представленный в виде y = f(t) на рисунке 2.

Для данного распределения вероятность безотказной работы определяется, как:

_{2 2}

P(t) = ^{-(t – m) / (2 σ)}·dt = 0,5 – Ф₀((t – m)/σ),

где Ф₀ – функция Лапласа, значение которой определяется по таблицам.

Рисунок 2. Характер изменения плотности вероятности безотказной работы f(t) и интенсивности отказов λ(t) при нормальном законе распределения времени до отказа

Дата добавления: 2014-01-05