Оценивание продолжительности операций

План лекции

1. Оценивание продолжительности операций

2. Параметры сетевой модели

Основу анализа сетевой модели составляет расчет значений ее параметров.

Параметры сетевой модели - величины, характеризующие временные соотношения между событиями и операциями, а также вид, количество ресурсов, затрачиваемых в процессе выполнения операций, и объем выполняемых работ.

Параметры, описывающие временные соотношения между событиями и операциями в сетевой модели, а также затраты времени на выполнение операций, называются временными параметрами. Исходными для определения всех временных параметров служит продолжительность (длительность) операции, обозначаемая t. для операции < i, j>. Продолжительность любой операции до окончания ее выполнения является величиной неизвестной, а следовательно, случайной. Наиболее полно случайная величина характеризуется законом распределения. Точные законы распределения продолжительностей операций, входящих в моделируемый комплекс, также обычно неизвестны. Поэтому на практике используют аппроксимирующие законы, которые стараются подобрать таким образом, чтобы один и тот же закон распределения, различаясь только числовыми характеристиками, с точностью, достаточной для целей моделирования, аппроксимировал законы рас­пределения продолжительностей всех операций, входящих в комплекс.

Наиболее часто в качестве аппроксимирующих законов используют законы бета-распределения, треугольного и логарифмически нормального распределений.

В общем случае формула плотности бета-распределения случайной величины x, заданной на интервале (0,1], имеет следующий вид:

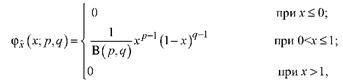(1)

где B(p, q) - бета-функция, определяемая выражением

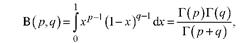(2)

где r(z) - гамма-функция, определяемая по формуле

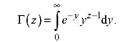(3)

Известно, что для целых z функция r(z) определяется выражением

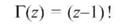(4)

Математическое ожидание, дисперсия и мода случайной величины, распределенной по закону (1), вычисляются по формулам

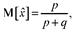
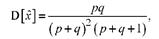
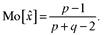
Величины p и q называются параметрами закона распределения (1). Если для аппроксимации реальных распределений продолжительностей операций используют бета-распределение, то поступают следующим образом Полагают, что продолжительность tj произвольной операции есть заданная на интервале

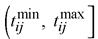
случайная величина, наиболее вероятное значение которой равно m, т. е.

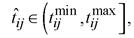
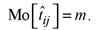
Введя параметры а = p - 1, у = q - 1 и задавая линейное преобразование случайной величины x в случайную величину tj выражением

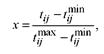
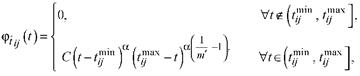
Дата добавления: 2014-01-05