Параметры сетевой модели

В основе определения параметров сетевой модели лежит понятие пути. Сетевая модель представляет собой ориентированный граф, поэтому путем в сети будет любая последовательность дуг, в которой начало непосредственно последующей дуги совпадает с концом непосредственно предшествующей. В детерминированной сети отсутствуют петли и контуры, следовательно, любой путь проходит через любую дугу и любую вершину не более одного раза. Это означает, что все пути в сетевой модели являются простыми и элементарными.

В сетевом моделировании используются следующие виды путей: между вершинами, предшествующий вершине, последующий за вершиной, полный.

Путь между вершинами - путь, исходящий из одной рассматриваемой вершины и входящий в другую рассматриваемую вершину.

Путь между вершинами i и j обычно обозначают символом L.

Путь, предшествующий вершине - путь между исходной и рассматриваемой вершинами.

При обозначении исходной вершины символом I путь, предшествующий вершине i, обозначается символом I_Ir

Путь, последующий за вершиной - путь между рассматриваемой и завершающей вершинами.

При обозначении завершающей вершины символом C путь, после­дующий за вершиной i, обозначается символом L;C.

Полный путь - это путь между исходной и завершающей вершинами.

Обычно полный путь обозначается символом L_IC Среди полных путей в сетевой модели ввиду особой важности выделяют критические и подкритические пути.

Критический путь - полный путь, имеющий в сетевой модели наибольшую продолжительность.

Подкритическим путем называют путь, продолжительность которого мало отличается от продолжительности критического пути. Это отличие чаще всего измеряется в долях от продолжительности критического пути и для всех подкритических путей не должно превышать заданного.

Для критического пути введем обозначение L_Kp. При анализе сетевых моделей наибольшее применение находят следующие параметры сети.

1. Продолжительность t(L_tJ) пути L_x. между вершинами i и j

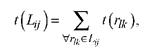
где r_lk - операция </, k>; t(r_lk) - продолжительность операции </, k>.

Продолжительность пути равна сумме продолжительностей операций, составляющих рассматриваемый путь.

Контрольные вопросы:

1. Что такое сетевая модель?

2. Что такое критический путь?

3. Что такое подкритический путь?

Тема № 3 «Модели и свойства элементарных систем массового обслуживания»

Лекция № 5 «Понятие системы массового обслуживания»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

Дата добавления: 2014-01-05