Понятие системы массового обслуживания

План лекции

1. Понятие системы массового обслуживания

2. Классификация систем массового обслуживания.

3. Простейший поток событий и его свойства

Объектом изучения теории массового обслуживания (ТМО) являются процессы обработки поступающих потоков сообщений системами массового обслуживания, а именно их количественные характеристики. Примерами систем массового обслуживания могут служить телефонные станции, локальные и глобальные вычислительные сети и т.п.

Основы новой теории были заложены в трудах датского математика, А. К. Эрланга (принцип статистического равновесия) и получили дальнейшее развитие в работах многих отечественных и зарубежных ученых.

Математическая модель системы массового обслуживания (СМО) включает четыре основных элемента: поток поступающих сообщений, систему обслуживания, характеристики качества и дисциплину обслуживания.

Понятие потока сообщений включает информацию о модели потока вызовов (требований на соединение), законе распределения, длительности обслуживания (передачи) сообщений, множестве адресов источников и приемников сообщений, а так же типе занимаемого для передачи сообщений канала и способе передачи - аналоговом или дискретном. Система обслуживания характеризуется структурой построения и набором структурных параметров. Под дисциплиной обслуживания поступающих сообщений понимают: способ обслуживания (с явными потерями, ожиданием, повторением или комбинированный), порядок обслуживания (в порядке очередности, случайном порядке или с приоритетом), а также другую информацию, характеризующую взаимодействие потока сообщений с системой обслуживания. К характеристикам качества обслуживания относятся:

1. Вероятность явной или условной потери сообщения

2. Среднее время задержки сообщения

3. Средняя длинна очереди

4. Вероятность потери поступившего вызова

5. Интенсивность обслуженной нагрузки и др.

При исследовании СМО могут решаться:

1. задачи анализа СМО - определение характеристик качества обслуживания в зависимости от параметров и свойств входящего потока сообщений, параметров и структуры системы обслуживания и дисциплины обслуживания;

2. задачи параметрического синтеза - определение параметров системы обслуживания при ее заданной структуре в зависимости от параметров и свойств потока сообщений, дисциплины и качества обслуживания.

3. задачи синтеза структуры системы с оптимизацией ее параметров таким образом, чтобы при заданных потоках, дисциплине и качестве обслуживания стоимость СМО была минимальной, либо были минимальными потери вызовов при заданных потоках, дисциплине и стоимости системы.

Математический аппарат теории массового обслуживания информации базируется на теории вероятностей, комбинаторике и математической статистике. Методы последней применяются в основном для обработки данных, получаемых при измерении параметров потоков сообщений и показателей качества обслуживания в реальных системах, а также при моделировании таких систем на ЭВМ. Для решения конкретных задач используются также сведения из других разделов математики, а именно: линейной алгебры, дифференциального и интегрального исчисления, теории графов, системного анализа.

Основным инструментом исследования в ТМО является метод уравнений вероятностей состояний, основанный на принципе статистического равновесия. Для системы обслуживания вводится понятие состояния. В простейшем случаесостояние системы характеризуется одной случайной переменной, например числом занятых линий или вызовов, находящихся на обслуживании и в очереди.

При поступлении очередного вызова, окончании обслуживания сообщения или изменении фазы работы управляющего устройства система меняет свое состояние. Интенсивности перехода из одного состояния в другое обычно известны на основании свойств потоков вызовов и освобождений. Это позволяет построить размеченный граф состояний и составить систему уравнений, связывающих между собой вероятности соседних состояний. Систему можно решить аналитически или численно.

При отсутствии аналитического решения в ряде случаев удается построить вычислительный алгоритм на основе рекуррентных соотношений, получаемых непосредственно из системы уравнений.

2. Классификация систем массового обслуживания.

В каждую систему массового обслуживания (СМО) поступает входящий поток заявок на обслуживание. Результатом работы СМО является выходящий поток обслуженных заявок.

Потоком заявок (событий) называется последовательность однородных событий, происходящих в какие-то случайные моменты времени.

Если в СМО одновременно может обслуживаться несколько заявок, то СМО называется многоканальной, в противном случае СМО называется одноканальной.

Как одноканальные СМО, так и многоканальные СМО делятся на СМО с отказами и СМО с очередью (ожиданием).

В СМО с отказами заявка, поступившая в момент, когда все каналы обслуживания заняты, получает «отказ» в обслуживании и покидает СМО.

В СМО с очередью заявка, поступившая в момент, когда все каналы обслуживания заняты, становится в очередь из заявок, ожидающих обслуживания. Как только один из каналов обслуживания освобождается, к обслуживанию принимается одна из заявок, стоящих в очереди.

СМО с очередью различаются по принципу построения (дисциплине) очереди.

Принципом построения очереди называется схема, в соответствии с которой заявки из очереди выбираются на обслуживание. Чаще всего при этом используется:

Случайный выбор заявки из очереди;

Выбор заявки из очереди в зависимости от её приоритета;

Выбор заявки в зависимости от порядка её поступления в очередь.

В третьем случае заявки из очереди могут обслуживаться, как по схеме: «Первым пришел - первым обслуживаешься», так и по схеме: «Последним пришел - первым обслуживаешься».

СМО с очередью делятся также на СМО с неограниченным ожиданием и СМО с ограниченным ожиданием.

В СМО с неограниченным ожиданием каждая заявка, поступившая в СМО, рано или поздно будет обслужена.

В СМО с ограниченным ожиданием на пребывание заявок в очереди накладываются различного рода ограничения. Эти ограничения могут касаться, например, длины очереди, времени пребывания заявки в очереди, общего времени пребывания заявки в СМО и т.п. В частности, в СМО с ограниченным временем пребывания в очереди, заявка, израсходовавшая лимит времени пребывания в очереди, покидает СМО.

Для систем массового обслуживания существенными, характеристиками, определяющими процессы в СМО, являются:

— тип входящего потока заявок (простейший, нестационарный пуассоновский и т. д.);

— закон распределения времени обслуживания (показательный, произвольный и т. д.);

— число параллельно включенных каналов обслуживания. Кроме того, важное значение имеют такие характеристики, как структура системы (разомкнутая или замкнутая) и принятая в системе дисциплина обслуживания.

В теории СМО принято классифицировать СМО с помо­щью трехбуквенного сокращения вида А\В\ т, где А и В опи­сывают соответственно распределение интервалов времени во входном потоке заявок и времени их обслуживания, а m — число обслуживающих приборов. Символы А и В представля­ют переменные, принимающие значения из следующего набора: символов, которые следует интерпретировать как соответству­ющие распределения

М — показательное распределение (Marcovian)

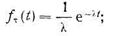
D — постоянная величина (Determinate)

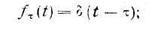
G — произвольное распределение (General).

3. Простейший поток событий и его свойства.

Поток событий называется простейшим потоком событий, если он об­ладает следующими свойствами стационарности, отсутствия последействия и ординарности:

1. Поток событий называется стационарным, если вероятность появ­ления одного или нескольких событий на участке времени длины T зависит только от длины T этого участка и не зависит от того, в каком месте оси вре­мени этот участок располагается.

2. Поток событий называется потоком с отсутствием последействия (без последействия), если события, составляющие поток, появляются в слу­чайные моменты времени независимо друг от друга.

3. Поток событий называется ординарным, если события, составляющие поток, происходят поодиночке, а не парами, тройками и т.д.

Замечание. Поток, в котором события происходят через равные промежутки времени, не является простейшим потоком событий!

• Интенсивностью (плотностью) потока событий называется среднее число событий, происходящих в единицу времени.

Замечание. Простейший поток событий обладает постоянной интенсив­ностью.

Контрольные вопросы:

1. Что называется потоком заявок?

2. Как классифицируются системы массового обслуживании?

3. Что называется принципом построения очереди?

4. Какой поток событий называется простейшим?

5. Какой поток событий называется стационарным?

Тема № 3 «Модели и свойства элементарных систем массового обслуживания»

Лекция № 6 «Структура системы массового обслуживания»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

Дата добавления: 2014-01-05