План лекции. 1. Структура и состав элементов системы массового обслуживания

1. Структура и состав элементов системы массового обслуживания

2. Источники и потоки заявок

1. Структура и состав элементов системы массового обслуживания.

При описании и анализе систем массового обслуживания (СМО) используется специальная терминология. Основными элементами СМО являются источник, генерирующий поток заявок на обслуживание, накопитель, обеспечивающий размещение в нем очереди заявок, ожидающих обслуживания и, наконец, каналы, или приборы, в которых производится процесс обслуживания заявок.

Принципиальная структура СМО приведена на рис. 1.

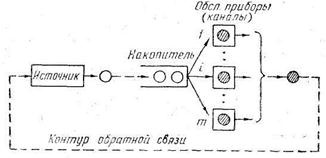
Рис. 1. Схема системы массового обслуживания

Из этой схемы видно, что обслуженные заявки могут снова возвращаться в источник, откуда поступать для нового обслуживания.

В общем случае в состав СМО может входить несколько источников, генерирующих потоки заявок, несколько накопителей-приборов обслуживания, связанных между собой. Такую систему называют сетью массового обслуживания. С помощью сетей МО могут моделироваться сети ЭВМ, автоматизированные системы управления в случае, когда в их состав входит совокупность объектов АСУ, связанных каналами передачи данных, различного рода коммуникационные системы, например, система воздушного движения, включающая совокупность аэропортов и связывающих их воздушных трасс.

Свойства СМО определяются ее структурой и характеристиками входящих в СМО элементов, в первую очередь источника, генерирующего поток заявок, и каналов, осуществляющих их обслуживание. Рассмотрим свойства и математические модели этих элементов

2. Источники и потоки заявок.

Под источником понимается любой объект, генерирующий заявки на обслуживание. На объекте АСУ это может быть оператор автоматизированного рабочего места, программа, выполняемая в ЭВМ КСА, некоторый источник прерываний (таймер, схема или программа контроля и т. д.). Различают два вида источников:

1) источники, у которых характеристики генерируемого потока заявок не зависят от процессов в системе обслуживания;

2) источники, поведение которых (т.е. свойства генерируемых ими потоков заявок) зависит от того, как происходит обслуживание заявок этих потоков.

Источники первого типа называются бесконечными, второго типа — конечными. Соответственно СМО по своей структуре делятся на разомкнутые и замкнутые.

Поток заявок, поступающих из источника на вход накопителя СМО, представляет последовательность событий (zn tn), где zn— заявка с номером п, п = 1, 2, 3,..., tn — момент ее возникновения. В теории СМО моменты t1 t2,... возникнове­ния заявок zi, рассматриваются как случайные моменты времени, поэтому поток заявок определяется как случайный процесс, задаваемый функцией распределения интервалов времени между соседними заявками

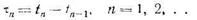
Предполагается, что каждый интервал tn представляет случайную величину, описываемую функцией распределения

где t — независимая переменная.

Поток заявок может быть нестационарным, если его характеристики изменяются во времени, и стационарным в противном случае. В реальных системах потоки заявок на входе СМО, как правило, нестационарны, поскольку их интенсивность зависит от конкретной ситуации, времени суток и года и т. д. Однако характеристики процессов обслуживания в СМО наиболее просто определяются для стационарных потоков, поэтому нестационарные действительные потоки при анализе аппроксимируются на отдельных интервалах времени стационарными.

Важнейшей вероятностной моделью входного потока заявок является модель в виде простейшего потока, т. е. в виде стационарного пуассоновского процесса. Для простейшего потока вероятность того, что в интервале времени Т поступит ровно k заявок, определяется распределением Пуассона

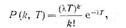(4.1)

где l — параметр, называемый интенсивностью потока заявок.

Для простейшего потока, описываемого распределением (4.1), интервалы t между соседними моментами заявок представляют независимые, случайные величины, подчиненные показатель­ному закону распределения с плотностью

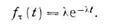(4.2)

Математическое ожидание и дисперсия для рас­пределения (4.2) равны:

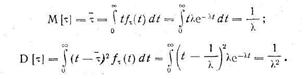
Простейший поток, помимо стационарности, обладает следующими свойствами:

— отсутствием последействия, проявляющего в том, что длина интервала t до момента поступления следующей заявки не зависит от того, поступила или нет заявка в рас­сматриваемый начальный момент времени;

— ординарностью, состоящей в том, что в каждый малый интервал времени может поступить не более одной заявки.

Рассмотрим указанные свойства более подробно. Образно говоря, отсутствие последствия показательно распределенного интервала времени состоит в том, что «возраст» интервала никак не влияет на величину оставшегося времени его «жизни». Пусть заявка поступила в момент t= 0. Распределение длины интервала до поступления следующей заявки описыва­ется выражением

Пусть, далее, с момента t = 0 прошло То секунд и не поступило ни одной заявки. Возникает вопрос: «Какова вероятность того, что следующая заявка поступит через t секунд, считая от момента Т0?». На основании теоремы о произведении вероятностей здесь имеем

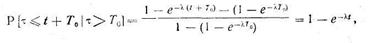(4.3)

Назовем величину интервала t длительностью «жизни» интервала, величину То — «возрастом» интервала, а разность t-То — остаточным временем жизни интервала. Соотношение (4.3) выражает тот факт, что для интервала, длительность жизни которого распределена по показательному зако­ну, остаточное время жизни интервала t-То имеет то же самое распределение.

Рассматриваемое свойство показательного распределения объясняется замечательным свойством показательной функции exp(-lt) состоящей в том, что любой ее «хвост» имеет с точностью до постоянного множителя форму самой функции, сдвинутой на соответствующую величину вправо по оси абсцисс. Действительно, пусть длина интервала имеет показательное распределение f(t)=lexp(-lt), а возраст равен Tо. Для того чтобы определить распределение остаточного времени интервала, нужно рассмотреть значения функции f(t) для t>T0.

Разделим все ординаты «хвоста» функции lexp(-lt), для t>T0 на площадь этого хвоста 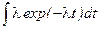равную, очевидно, вероятности Р[t>T0]. Эта операция тождественна операции вычисления условного распределения путем деления вероятности совместного события (Т0<t <t + To) на вероятность условия, т. о. события (t>T0). Получающая в результате деления функция

представляет точную копию исходной функции f(t), но сдвинутую из нулевой точки вправо на Tо единиц времени, т. е. функцию

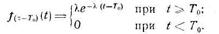
Полученный результат подтверждает свойство ординарности-простейшего потока, состоящее в том, что вероятность попадания в короткий интервал 0 двух и более заявок для простейшего потока много меньше вероятности попадания одной заявки, равной .

В теории массового обслуживания наибольшее число результатов получено именно для простейшего входного потока заявок. Это обстоятельство, а также тот факт, что простейший поток в силу своей предельной нерегулярности создает наиболее тяжелый режим работы для СМО, привели к тому, что анализ процессов функционирования СМО, как правило,, рассматривается именно для этого типа входного потока.

Контрольные вопросы:

1. Назовите основные элементы системы массового обслуживания?

2. Назовите типы источников заявок в СМО?

3. Какими свойствами обладает простейший поток заявок?

Тема № 3 «Модели и свойства элементарных систем массового обслуживания»

Лекция № 7 «Процессы в системах массового обслуживания»

Цель лекции.

а) учебная цель:

Целью является формирование у слушателей целостного представления о принципах применения элементов теории вероятностей при моделировании сетевых процессов – элемента систем массового обслуживания.

Дата добавления: 2014-01-05