
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Устойчивые неминимально-фазовые звенья
|
|
|
|
В ряде устройств, например при дифференциальных или мостовых соединениях, встречаются звенья, описываемые дифференциальными уравнениями, имеющими отрицательные коэффициенты в правой части уравнения и соответственно нули в правой полуплоскости. При этом фазовый сдвиг между входным и выходным сигналами может превышать  .
.
Дифференциальное уравнение устойчивого неминимально-фазового звена первого порядка имеет вид
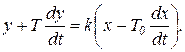 (1.7.60)
(1.7.60)
Комплексный коэффициент усиления такого звена
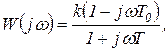 (1.7.61)
(1.7.61)
а передаточная функция
 (1.7.62)
(1.7.62)
Примерами таких звеньев могут служить мостовые схемы, изображенные на рисунке 1.7.16. В случае (а) уравнение имеет вид
 (1.7.63)
(1.7.63)
а в случае (б)
 (1.7.64)
(1.7.64)
Здесь  , а
, а 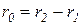 . В обоих случаях имеется в виду, что
. В обоих случаях имеется в виду, что  .
.
Для схемы (а)  ,
,  ,
,  ,
, 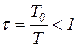 .
.
Для схемы (б)  ,
,  ,
, 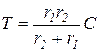 ,
, 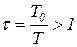 .
.
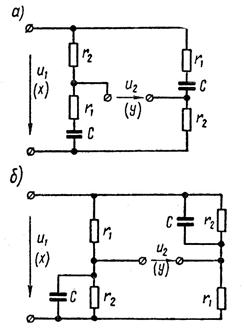
Рисунок 1.7.16 – Примеры неминимально-фазовых звеньев
На рисунке 1.7.17 построены частотные характеристики рассматриваемого звена. Построение выполнено для нормированных характеристик  и
и 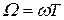 при
при  и
и 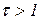 .
.
Как видно из построения, при  и при
и при 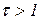 частотные годографы лежат в третьем и четвертом квадрантах, имея вид полуокружностей. Соответственно инверсные характеристики представляют собой полуокружности, лежащие в первом и втором квадрантах.
частотные годографы лежат в третьем и четвертом квадрантах, имея вид полуокружностей. Соответственно инверсные характеристики представляют собой полуокружности, лежащие в первом и втором квадрантах.
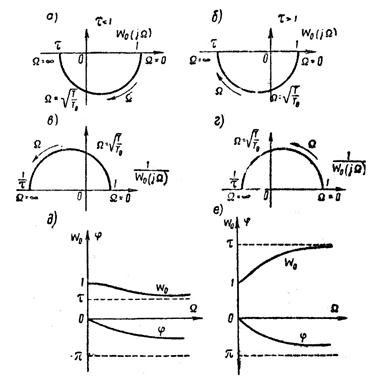
Рисунок 1.7.17 – Характеристики устойчивого неминимально-фазового звена
При различном расположении годографов 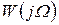 для инерционно-форсирующего (см. рисунок 1.7.12) и неминимально-фазового рассматриваемого звена их амплитудно-частотные характеристики аналогичны. Действительно, в рассматриваемом случае
для инерционно-форсирующего (см. рисунок 1.7.12) и неминимально-фазового рассматриваемого звена их амплитудно-частотные характеристики аналогичны. Действительно, в рассматриваемом случае
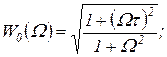 (1.7.65)
(1.7.65)
что полностью совпадает с формулой (1.7.44).
Для фазочастотных характеристик
 (1.7.66)
(1.7.66)
что существенно отличается от (1.7.45).
Таким образом, при совпадении амплитудно-частотных характеристик минимально-фазовых и неминимально-фазовых звеньев их фазочастотные характеристики не совпадают.
По передаточной функции (1.7.62) может быть найдена переходная функция (рисунок 1.7.18, а)
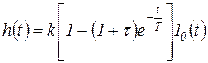 (1.7.67)
(1.7.67)
и весовая функция (рисунок 1.7.18, б)
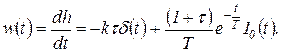 (1.7.68)
(1.7.68)
Из рисунка видно, что  в зависимости от времени меняет знак, однако в отличие от аналогичных характеристик минимально-фазовых звеньев величина τ не оказывает столь существенного влияния на ход кривых
в зависимости от времени меняет знак, однако в отличие от аналогичных характеристик минимально-фазовых звеньев величина τ не оказывает столь существенного влияния на ход кривых  и
и 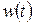 .
.
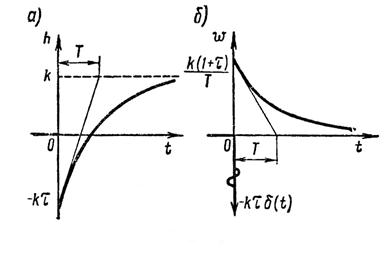
Рисунок 1.7.18 – Переходная (а) и весовая (б) функции устойчивого
неминимально-фазового звена
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 824; Нарушение авторских прав?; Мы поможем в написании вашей работы!