Иррациональные звенья

Особые звенья: иррациональные и трансцендентные звенья

Звено с распределенными параметрами, описываемое одно­мерным урав­нением теплопроводности Фурье

(1.7.79)

где 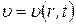— величина, зависящая от пространственной координаты r и времени t, имеет иррациональную передаточ­ную функцию, вид которой существенно зависит от гранич­ных условий, учитывающих входной сигнал и место снятия выходного сигнала.

Рассматривая величину как синусоидально изменяющуюся с частотой ω, т.е. , фазор которой

(1.7.80)

уравнение (1.7.79) можно преобразовать следующим образом:

(1.7.81)

Это однородное дифференциальное уравнение, имеющее корни характеристического уравнения

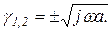(1.7.82)

Решение уравнения (1.7.81) имеет вид

(1.7.83)

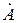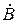где и — коэффициенты, зависящие от граничных условий.

Если граничным условием является 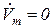при , то и

(1.7.84)

Наиболее характерны три случая приложения входных и снятия выходных воздействий:

(1.7.85)

что соответствует граничным условиям первого рода;

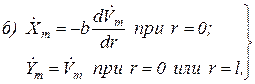(1.7.86)

что соответствует граничным условиям второго рода;

(1.7.87)

что соответствует граничным условиям третьего рода.

Комплексный коэффициент усиления звена опреде­ляется как с учётом уравнения (1.7.84). При этом постоянная A сокращается, и для трёх рассмотренных случаев получаем:

в случае (а)

(1.7.88)

в случае (б)

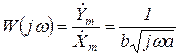(1.7.89)

или

(1.7.90)

в случае (в)

(1.7.91)

или

(1.7.92)

Во всех случаях комплексный коэффициент усиления выра­жается иррациональной функцией .

Примерами иррацио­нальных звеньев могут служить различные диф­фузионные и тепловые объекты (рисунок 1.7.21, а), объекты индук­ционного нагрева, теле­фонный кабель (рисунок 1.7.21, б) с распределенными сопро­тивлением и ёмкостью.

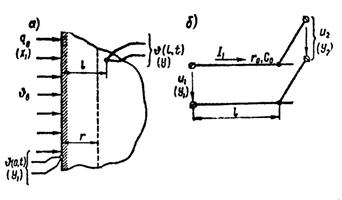
Рисунок 1.7.21 – Примеры иррациональных звеньев

Передаточными функциями, соответствующими выражени­ям (1.7.89), (1.7.91) и (1.7.88) при , , и 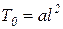, будут:

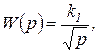(1.7.93)

(1.7.94)

(1.7.95)

Выражения (1.7.93) и (1.7.94) отличаются от передаточных функций интегрирующего и инерционного звеньев только квадратным корнем. По аналогии с интегрирующими и инер­ционными такие звенья можно назвать полуинтегрирующими и полуинерционными. Третье выражение не только иррационально, но и трансцендентно.

Рассмотрим характеристики иррациональных звеньев, опи­сываемых уравнениями (1.7.93) и (1.7.94).

Полуинтегрирующее звено. Частотные характе­ристики полуинтегрирующего звена, построенные по уравне­нию

(1.7.96)

показаны на рисунке 1.7.22. Частотный годограф (а) имеет вид прямей линии, лежащей в четвертом квадранте и идущей под углом 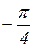, т.е. под углом в два раза меньшим, чем для интегрирующего звена. Соответственно инверсная характеристика (б) лежит в первом квадранте и идет под углом .

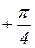Рисунок 1.7.22 – Характеристики полуинтегрирующего звена

Амплитуда и фаза комплексного коэффициента усиления описываются выражениями следующего вида:

(1.7.97)

и

(1.7.98)

Графики амплитудно-частотных и фазочастотных характеристик показаны на рисунке 1.7.22, в и г.

Пере­ходная и весовая функции (рисунок 1.7.22, г и д):

(1.7.99)

и

(1.7.100)

Если в интегрирующем звене за время 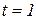величина h вырастает до величины (пунктир на рисунке 1.7.22, г), то в полуинтегрирующем звене вначале процесс протекает быстрее, и за время 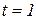величина h достигает значения . С течением времени в полуинтегрирующем звене так же, как и в интегрирующем, , т.е. нет самовыравнивания.

Полуинерционное звено. Частотные характеристики полуинерционного звена показаны на рисунке 1.7.23, а, б, в. Здесь

(1.7.101)

Годограф полуинерционного звена (а) в отличие от годо­графа инерционного звена представляет собой не половину, а четверть окружности с центром в точке O, опирающуюся на хорду длиной k. Касательные к годографу в точках 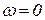и образуют с вещественной осью углы и пересе­каются под углом .

Инверсная характеристика (б) представляет собой полу­прямую, выходящую из точк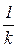и при 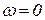под углом вещественной оси.

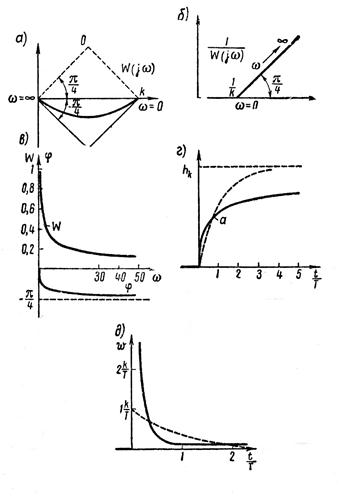
Рисунок 1.7.23 – Характеристики полуинерционного звена

Модуль и фаза комплексного коэффициента усиления (рисунок 1.7.23, в) соответственно будут:

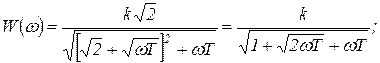(1.7.102)

(1.7.103)

При .

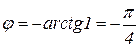Переходная функция полуинерционного звена определяется выражением

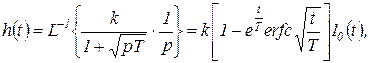(1.7.104)

где 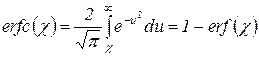— табулированный интеграл вероятности.

Весовая функция

(1.7.105)

Обе эти функции построены на рисунке 1.7.23, г и д. Там же пунктиром показаны аналогичные характеристики для инерци­онного звена.

Как видно из графика, полуинерционное звено является звеном с самовыравниванием, однако в отличие от инерцион­ного звена при той же постоянной времени Т переходный про­цесс полуинерционного звена вначале идет быстро, а затем — более медленно приближается к установившемуся режиму. Значение выходной величины, которое достигается в полуинер­ционном и инерционном звеньях за одинаковое время, соответ­ствует 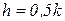при 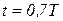(см. точку пересечения а на рисунке 1.7.23, г).

Дата добавления: 2014-01-05