Трансцендентные звенья

Звено с распределенными параметрами, описываемое одно­мерным телеграфным уравнением Даламбера

(1.7.106)

где 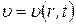— величина, зависящая от пространственной координаты r и времени t, имеет трансцендентную передаточ­ную функцию, которая зависит от граничных условий и места снятия выходного сигнала.

Рассматривая зависящий от пространственной координаты фазор

(1.7.107)

можно уравнение (1.7.106) привести к виду

(1.7.108)

Корни характеристического уравнения — мнимые

(1.7.109)

где .

Решение уравнения (1.7.108) можно записать как

(1.7.110)

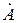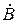где и — коэффициенты, зависящие от граничных условий. Первое слагаемое выражает волну, движущуюся в сторону возрастания r, второе — обратную волну, движущуюся в сто­рону убывания r.

Звено запаздывания. Ограничимся рассмотрением таких объектов, в которых имеется только одна волна, движущаяся в сторону возрастания r. Тогда и

(1.7.111)

Наиболее распространенным случаем является приложение входного воздействия при , т.е. , и снятие выходного сигнала при , т.е. 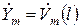. В таком случае , и

(1.7.112)

где — время запаздывания.

Если или , то или , т.е. выходная величина воспроизводит входной сигнал с отставанием во времени на время запаздывания τ.

Примеры звеньев запаздывания можно встретить в самых различных технологических конвейерных установках, в систе­мах магнитной записи и воспроизведения, в гидравлических системах и в электрических це­пях без потерь с распределен­ными индуктивностью и ём­костью .

Некоторые примеры реальных звеньев запаздывания показаны на рисунке 1.7.24. При загрузке сыпу­чего материала на конвейер (а), движущийся со скоростью , толщина слоя , находящегося на расстоянии l, отстает от тол­щины слоя 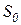, находящегося в начале, на время . Напря­жение на зажимах считывающей головки (б) магнитной системы воспроизводит напряжение записывающей системы с запаздыва­нием . Напряжение в конце линии без потерь (в) на­груженной на согласованное сопротивление 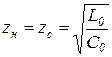, воспроизводит напряжение в начале, линии с запаздыванием .

Рисунок 1.7.24 – Примеры звена запаздывания

Частотные характеристики комплексного коэффициента уси­ления, рассчитанные по формуле (1.7.112), показаны на рисунке 1.7.25, а и б. Амплитудно-фазовая характеристика представ­ляет собой окружность единичного радиуса с центром в начале координат (а). Окружность пересекает вещественную ось в точке 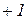при и в точке при .

Амплитудно-частотные и фазочастотные характеристики (б) определяются следующими соотношениями:

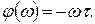
Передаточная функция звена запаздывания

(1.7.113)

Рисунок 1.7.25 – Характеристики звена запаздывания

Звено запаздывания является неминимально-фазовым устой­чивым звеном. Оно имеет бесконечное множество полюсов, лежащих в левой полуплоскости, с модулем, стремящимся к бесконечности, и бесконечное множество нулей, лежащих в правой полуплоскости, с модулем, также стремящимся к бесконечности. Действительно, уравнение имеет решение , если и , а уравнение , если и (см. рисунок 1.7.26).

Рисунок 1.7.26 – Расположение нулей и полюсов звена запаздывания

Переходная и весовая функции (рисунок 1.7.25, в и г) имеют вид

(1.7.114)

(1.7.115)

Звено затухания (или полузапаздывания). Несколько более сложно выражаются характеристики иррационального звена, описываемого показательной передаточной функцией (1.7.95). Такое звено может быть условно названо звеном затухания, так как в отличие от звена запаздывания в нем сигнал на выходе всегда меньше сигнала на входе. Оно также не является минимально-фазовым, поскольку функция имеет нули в правой полуплоскости при .

Амплитудно-фазовая характеристики звена имеет вид:

(1.7.116)

На рисунке 1.7.27, а, б построены амплитудно-фазовая, амплитудно-частотная и фазочастотная характеристики. Комп­лексный коэффициент усиления при изменении аргумента на уменьшается по модулю в раз. Зависимость ампли­туды и фазы от частоты получается непосредственно из (1.7.116)

(1.7.117)

(1.7.118)

Рисунок 1.7.27 – Характеристики звена затухания

Переходная и весовая функции имеют вид

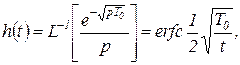(1.7.119)

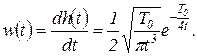(1.7.120)

Графики этих функций показаны на рисунке 1.7.27, в и г.

Дата добавления: 2014-01-05