
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Запись положительных рациональных чисел в виде десятичных дробей
|
|
|
|
Лекция 50. Десятичные дроби
План:
1. Десятичные дроби. Алгоритмы арифметических действий над ними.
2. Преобразование обыкновенных дробей в десятичные.
3. Рациональные числа как бесконечные десятичные периодические дроби.
4. Преобразование периодических десятичных дробей в обыкновенные.
В практической деятельности широко используются дроби, знаменатели которых являются степенями 10. Их называют десятичными.
Определение. Десятичной называется дробь вида 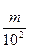 , где m и n - натуральные числа.
, где m и n - натуральные числа.
Десятичные дроби принято записывать без знаменателя. Например, дробь 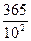 - записывают в виде 3,67, а дробь
- записывают в виде 3,67, а дробь 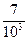 в виде 0,007.
в виде 0,007.
Выясним, как образуется такая запись. 10

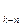

Пусть дана дробь 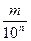 , где m и n - натуральные числа. Представим ее числитель в
, где m и n - натуральные числа. Представим ее числитель в
следующем виде:
m = a 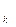 ∙ 10
∙ 10 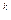 + a
+ a  ∙10
∙10 + …+ a
+ …+ a 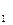 ∙10 + a ₀.
∙10 + a ₀.
Тогда, по правилам действий над степенями при n < k, получим:
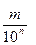 = a
= a 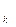 ∙ 10
∙ 10 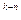 + a
+ a  ∙10
∙10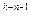 + …+ a
+ …+ a 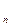 +
+ 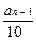 + … +
+ … +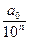 .
.
Сумма a 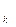 ∙ 10
∙ 10 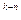 + a
+ a  ∙10
∙10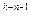 + …+ a
+ …+ a 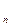 является записью целого неотрицательного числа (обозначим его буквой А), а сумма
является записью целого неотрицательного числа (обозначим его буквой А), а сумма 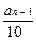 + … +
+ … +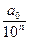
представляет дробную часть числа, ее принято записывать без знаменателя в виде а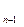 … a ₀. Таким образом, дробь —- можно представить в следующем виде: А, а
… a ₀. Таким образом, дробь —- можно представить в следующем виде: А, а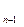 … a ₀, т.е. при записи дроби последние n цифр десятичной записи числа m отделяют запятой. Если числитель содержит менее чем n десятичных знаков, то перед ним пишут столько нулей, чтобы получилась n + 1 цифра, после чего отделяют запятой n знаков, начиная с конца. Например,
… a ₀, т.е. при записи дроби последние n цифр десятичной записи числа m отделяют запятой. Если числитель содержит менее чем n десятичных знаков, то перед ним пишут столько нулей, чтобы получилась n + 1 цифра, после чего отделяют запятой n знаков, начиная с конца. Например,
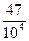 =
= 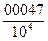 = 0,0047.
= 0,0047.
Как известно, сравнение десятичных дробей и арифметические действия над ними легко выполнять, если дроби имеют один и тот же знаменатель.
В основе приведения десятичных дробей к общему знаменателю лежит следующее утверждение: если к десятичной дроби А, а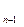 … a ₀, приписать справа любое число нулей, то получится десятичная дробь, равная данной.
… a ₀, приписать справа любое число нулей, то получится десятичная дробь, равная данной.
Это свойство позволяет приводить десятичные дроби к общему знаменателю следующим образом: если у одной дроби после запятой стоит n цифр, а у другой р цифр, причем n < р, то для приведения их к общему знаменателю достаточно к первой дроби приписать справа р- n нулей. Тогда у обеих дробей после запятой будет стоять поровну цифр, а это значит, что они имеют один и тот же знаменатель.
Пользуясь этим правилом, легко выполнять сравнение десятичных дробей, так как оно сводится к сравнению натуральных чисел: чтобы сравнить две десятичные дроби, надо уравнять в них число десятичных знаков после запятой, отбросить запятые и сравнить получившиеся натуральные числа.
Например, 4,62517 > 4,623, так как 4,623 = 4,62300, а 4,62517 > 4,62300, так как 462517 > 462300.
Как известно, для дробей, имеющих одинаковые знаменатели, сложение и вычитание сводится к соответствующим операциям над их числителями. Это позволяет свести сложение и вычитание десятичных дробей к действиям над натуральными числами.
Например,
2,54 + 3,7126 = 2,5400 + 3,7126 = 6,2526.
Умножение и деление десятичных дробей не требует приведения их к общему знаменателю, но они также сводятся к соответствующим действиям над натуральными числами.
Среди десятичных дробей выделяют и часто используют дробь 0,01. Ее называют процентом и обозначают 1%. Запись р % обозначает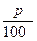 .
.
Например, 25% - это дробь 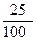 , или 0,25.
, или 0,25.
Проценты были введены, когда не существовало десятичных дробей. Чтобы производить расчеты по займам, определяли прирост капитала из расчета 100 денежных единиц. Этот прирост и называли числом процентов (рго сеntum - на сто).
Простота сравнения и выполнения действий над десятичными дробями приводит к следующему вопросу: любую ли дробь вида 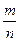
(m, n ÎN) можно записать в виде конечной десятичной дроби, т.е. дроби, у которой после запятой стоит конечное число цифр? Ответ на него дает следующая теорема.
Теорема. Для того чтобы несократимая дробь 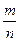 была равна десятичной, необходимо и достаточно, чтобы в разложение ее знаменателя и на простые множители входили лишь простые числа 2 и 5.
была равна десятичной, необходимо и достаточно, чтобы в разложение ее знаменателя и на простые множители входили лишь простые числа 2 и 5.
Так, например, дробь 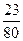 можно записать в виде десятичной: она 80
можно записать в виде десятичной: она 80
несократима и 80 = 2⁴∙5. Дробь 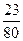 несократима, но 15 = 3∙5. Поскольку в разложение знаменателя этой дроби входит множитель, отличный от 2 и 5, то дробь — нельзя записать в виде десятичной.
несократима, но 15 = 3∙5. Поскольку в разложение знаменателя этой дроби входит множитель, отличный от 2 и 5, то дробь — нельзя записать в виде десятичной.
Дробь 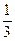 - нельзя представить в виде конечной десятичной дроби. Но, деля 1 на 3, получаем, что 0,3 <
- нельзя представить в виде конечной десятичной дроби. Но, деля 1 на 3, получаем, что 0,3 <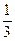 < 0,4. Далее находим, что 0,33 <
< 0,4. Далее находим, что 0,33 < 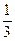 < 0,34; 0,333 <
< 0,34; 0,333 < 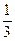 < 0,334 и т.д. Вообще для любого n имеем: 0,33...33<
< 0,334 и т.д. Вообще для любого n имеем: 0,33...33<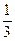 < 0.33...34
< 0.33...34
Вместо того чтобы писать бесконечное множество неравенств, говорят, что дроби 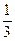 соответствует бесконечная десятичная дробь 0,33…3… Это означает, что если отбросить в бесконечной дроби все цифры, начиная с некоторой, то будем иметь число, меньшее
соответствует бесконечная десятичная дробь 0,33…3… Это означает, что если отбросить в бесконечной дроби все цифры, начиная с некоторой, то будем иметь число, меньшее 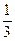 , а если в полученном числе увеличить последнюю цифру на 1, то будет число, большее
, а если в полученном числе увеличить последнюю цифру на 1, то будет число, большее 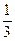 .
.
Любую конечную десятичную дробь можно записать в виде бесконечной, приписав к ней справа последовательность нулей. Например, дробь 0,25 можно записать так: 0,25000...0.... Здесь для всех цифр, начиная с некоторой, получится число, не превосходящее 0,25 (например, если оставить лишь одну цифру после запятой, то получится 0,2, меньшее 0,25, а если оставить три цифры после запятой, то будет число 0,250, равное 0,25). Если же после отбрасывания увеличить последнюю цифру на 1, то имеем число, большее 0,25 (например, 0,3 или 0,251).
Бесконечные десятичные дроби, которые получаются при записи положительного рационального числа, обладают особенностью - они являются периодическими. Это значит, что, начиная с некоторой цифры, они образуются бесконечным повторением одной и той же группы цифр. Например, число  выражается бесконечной десятичной дробью 0,272727...27..., а число
выражается бесконечной десятичной дробью 0,272727...27..., а число 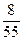 - бесконечной десятичной дробью 0,1454545...45.... Для краткости первую из дробей пишут в виде 0,(27), а вторую - в виде 0,1(45). В скобки заключают повторяющуюся группу цифр, которую называют периодом этой дроби. Отметим, что вместо 0,(27) можно было написать и 0,2(72), но эта запись более длинная. Приведенные рассуждения приводят к следующей теореме.
- бесконечной десятичной дробью 0,1454545...45.... Для краткости первую из дробей пишут в виде 0,(27), а вторую - в виде 0,1(45). В скобки заключают повторяющуюся группу цифр, которую называют периодом этой дроби. Отметим, что вместо 0,(27) можно было написать и 0,2(72), но эта запись более длинная. Приведенные рассуждения приводят к следующей теореме.
Теорема. Любое положительное рациональное число представимо бесконечной периодической десятичной дробью.
Доказательство. Пусть рациональное число представлено несократимой дробью —. Чтобы преобразовать ее в десятичную, надо выполнить деление натурального числа m на натуральное число n. При этом будут остатки, меньшие n, т.е. числа вида 0, 1, 2,... n - 1. Если хотя бы один из остатков окажется равным нулю, то после деления получится конечная десятичная дробь (или, что то же самое, бесконечная десятичная дробь, заканчивающаяся последовательностью нулей). Если же все остатки отличны от нуля, то деление будет представлять собой бесконечный процесс, но количество различных остатков конечно, и поэтому, начиная с некоторого шага, какой-то остаток повторится, что приведет к повторению цифр в частном.
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 854; Нарушение авторских прав?; Мы поможем в написании вашей работы!