Надежность в период постепенных отказов

Для постепенных отказов нужны законы распределения времени безотказной работы, которые дают вначале низкую плотность распределения, затем максимум и далее падение.

В этот период для описания надежности применяют несколько законов распределений.

Нормальное распределение является наиболее удобным и широко применяемым для практики (рис. 1.4).

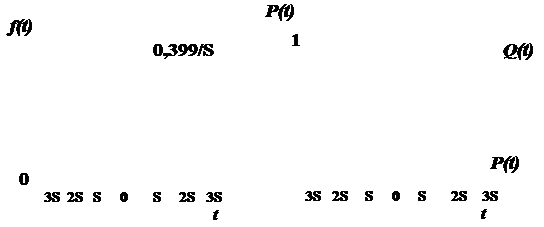
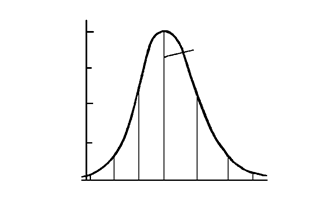
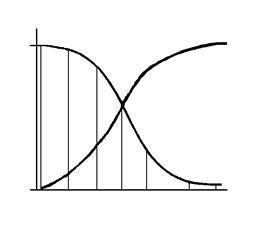
Рис. 1.4. Функция плотности вероятности и интегральная функция вероятности нормального распределения

Нормальному распределению подчиняется наработка до отказа многих восстанавливаемых и невосстанавливаемых изделий, размеры и ошибки измерений деталей и т. д.

Плотность распределения

.

Распределение имеет два независимых параметра: математическое ожидание m_t, наработка до отказа и среднее квадратическое отклонение S.

,

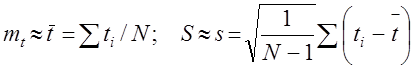где 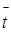и s – оценки математического ожидания и среднего квадратического отклонения.

Вероятность отказа за период времени до m_t – 3 S составляет всего 0,135 % и обычно не учитывается в расчетах. Наибольшая ордината кривой ния равна 0,399/S.

Интегральная функция распределения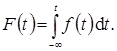

Вычисление интегралов заменяют использованием таблиц.

Помимо задачи оценки вероятности безотказной работы за данное время или за данную наработку встречается обратная задача – определение времени или наработки, соответствующих заданной вероятности безотказной работы.

Значение этой наработки (времени) определяют с помощью квантилей нормированного нормального распределения t = m_t + u _p S.

Значения квантилей даются в таблицах.

Пример. Оценить вероятность P(t) безотказной работы в течение t =1,5×10⁴ч изнашиваемого подвижного сопряжения, если ресурс по износу подчиняется нормальному распределению с параметрами m_t =4×10⁴ч, S =10⁴.

Решение. Находим квантиль 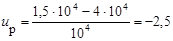; по таблице 1.1 определяем, что P(t) = 0,9938.

Пример. Оценить 80 %-ный ресурс t _0.8 гусеницы трактора, если известно, что долговечность гусеницы ограничена по износу, ресерс подчиняется нормальному распределению с параметрами

m_t = 10⁴ ч; S = 6×10³ч.

Решение. При P(t) = 0,8; u _p = - 0,84: t _0,8 = m_t + u _p S =10⁴-0,84×6×10³»5×10³ ч.

Таблица 1.1

Нормальное распределение	Распределение Вейбулла
Квантиль u p	Вероят-ность безотказ-ной работы Р(t)	Квантиль u p	Вероят-ность безотказ-ной работы Р (t)	Параметр формы т		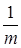bm	cm	Коэффи-циент вариации
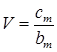
0,000	0,5000	-2,054	0,98	0,400	2,5	3,32	10,4	3,14
-0,1	0,5398	-2,1	0,9821	0,417	2,4	2,98	8,74	2,93
-0,126	0,55	-2,170	0,985	0,435	2,3	2,68	7,38	2,75
-0,2	0,5793	-2,2	0,9861	0,455	2,2	2,42	6,22	2,57
-0,253	0,60	-2,3	0,9893	0,476	2,1	2,20	5,27	2,40
-0,3	0,6179	-2,326	0,99	0,500	2,0	2,00	4,47	2,24
-0,385	0,65	-2,4	0,9918	0,526	1,9	1,83	3,81	2,08
-0,4	0,6554	-2,409	0,992	0,556	1,8	1,68	3,26	1,94
-0,5	0,6915	-2,5	0,9938	0,588	1,7	1,54	2,78	1,80
-0,524	0,70	-2,576	0,995	0,625	1,6	1,43	2,39	1,67
-0,6	0,7257	-2,6	0,9953	0,667	1,5	1,33	2,06	1,55
–0,674	0,75	–2,652	0,996	0,714	1,4	1,24	1,78	1,43
-0,7	0,7580	–2,7	0,9965	0,769	1,3	1,17	1,54	1,32
–0,8	0,7881	–2,748	0,997	0,833	1,2	1,10	1,33	1,21
–0,842	0,80	–2,8	0,9974	0,909	1,1	1,05	1,15	1,10
-0,9	0,8159	–2,878	0,998	1,0	1,0	1,00	1,00	1,00
-1,0	0,8413	–2,9	0,9981	1,1	0,909	0,965	0,878	0,910
–1,036	0,85	–3,0	0,9986	1,2	0,833	0,941	0,787	0,837
–1,1	0,8643	–3,090	0,999	1,3	0,769	0,924	0,716	0,775
–1,2	0,8849	–3,291	0,9995	1,4	0,714	0,911	0,659	0,723
–1,282	0,90	–3,5	0,9998	1,5	0,667	0,903	0,615	0,681
–1,3	0,9032	–3,719	0,9999	1,6	0,625	0,897	0,574	0,640
–1,4	0,9192			1,7	0,588	0,892	0,540	0,605
–1,5	0,9332			1,8	0,556	0,889	0,512	0,575
–1,6	0,9452			1,9	0,526	0,887	0,485	0,547
–1,645	0,95			2,0	0,500	0,886	0,463	0,523
–1,7	0,9554			2,1	0,476	0,886	0,439	0,496
–1,751	0,96			2,2	0,455	0,886	0,425	0,480
–1,8	0,9641			2,3	0,435	0,886	0,409	0,461
–1,881	0,97			2,4	0,417	0,887	0,394	0,444
-2,0	0,9772			2,5	0,400	0,887	0,380	0,428

Примечания: 1. Под t понимается время или другие случайные величины.

2. Для логарифмически нормального распределения u _p=(1n t – m)/ S.

В логарифмически нормальном распределении логарифм случайной величины распределяется по нормальному закону. Оно несколько точнее, чем нормальное, описывает наработку до отказа деталей, в частности, по усталости. Его успешно применяют для описания наработки подшипников качения, электронных ламп и других изделий.

Плотность распределения (рис. 1.5) описывается зависимостью

,

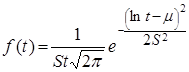где m. и S – параметры, оцениваемые по результатам испытаний. Так, при испытаниях N изделий до отказа

,

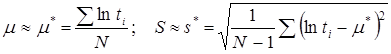где m * и s – оценка параметров m, и S.

0

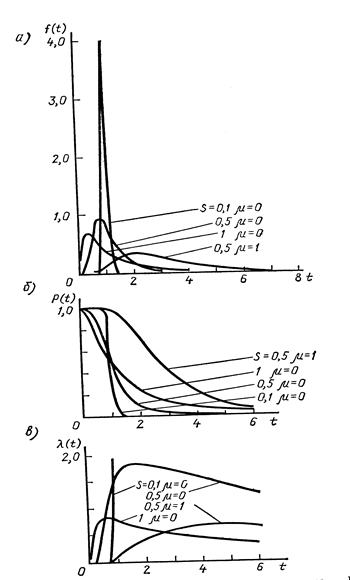
Рис.1.5 Основные характеристики логарифмически нормального распределения при разных параметрах: а) – плотность вероятности f(t); б) – вероятность безотказной работы P(t);

в) – интенсивность отказов l (t)

Вероятность безотказной работы можно определить по таблицам для нормального распределения (см.табл. 1.1) в зависимости от значения квантили u _p= (ln t–m)/S.

Математическое ожидание наработки до отказа

;

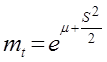среднее квадратическое отклонение

;

коэффициент вариации

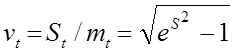
При V_t £ 0,3 полагают V_t» S, при этом ошибка £ 1%.

Распределение Вейбулла довольно универсально и охватывает широкий диапазон случаев изменения вероятностей. Оно удовлетворительно описывает наработку деталей по усталостным разрушениям, наработку до отказа подшипников, электронных ламп. Используется для оценки yflt;yjcnb автомобилей, подъемно-транспортных и других машин.

Распределение характеризуется функцией вероятности безотказной работы (рис. 1.6):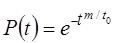

Интенсивность отказов

;

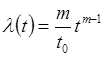плотность распределения

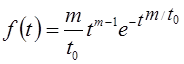
Распределение Вейбулла имеет два параметра: параметр формы m > 0 и параметр масштаба t ₀ > 0.

Математическое ожидание

;

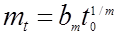среднее квадратическое отклонение

,

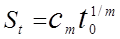где b_т и c_m— коэффициенты (см. табл. 1.1).

Если в течение времени t* отказы не наступают, то вероятность безотказной работы

.

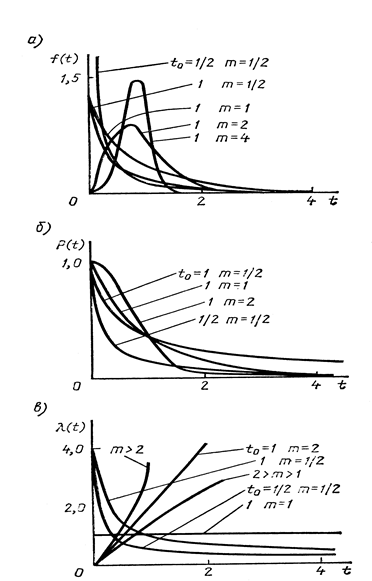
Рис. 1.6. Основные характеристики распределения Вейбулла при разных параметрах t ₀ и т:

а — плотность вероятности f (t); б — вероятность безотказной работы Р(t);

в — интенсивность отказов l (t)

Возможности и универсальность распределения Вейбулла видны из следующих пояснений (рис. 1.6).

При т <1 функции l (t) и f (t) от наработки до отказа убывающие.

При т =1 распределение экспоненциальное l(t)=const и f (t) — убывающая.

При т >1 f (t) - одновершинная, l (t) возрастающая при 1< m <2 с выпуклостью вверх, а при т>2 - с выпуклостью вниз.

При т =2 функция l(t) является линейной.

При m ==3,3 распределение Вейбулла близко к нормальному.

Пример. Оценить вероятность безотказной работы Р (t) роликоподшипников в течение t =10⁴ ч, если ресурс подшипников описывается распределением Вейбулла с параметрами t ₀=10⁷ ч, m =1,5.

Решение.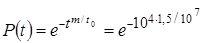=0,905

Дата добавления: 2014-01-06