Принцип включения и исключения

Пусть A₁,…,A_n некоторые подмножества (необязательно различные) конечного множества Х.

Теорема 1.(Принцип включения и исключения).

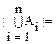
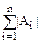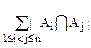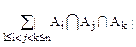-+-…(-1)^n-1||

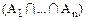Доказательство

Применим математическую индукцию по n.

Для n=1 терема очевидно справедлива!

Предположим, что для произвольных A₁,…,A_n-1 выполняется

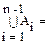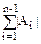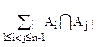||=-+-…(-1)^n-2||

Применяя эту формулу к сумме

,

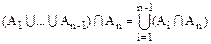получаем

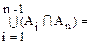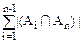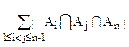||=-+…(-1)^n-2||,

а отсюда

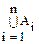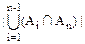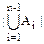||==+|A_n|-||=

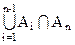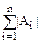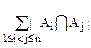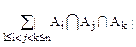-+-…(-1)^n-1||.

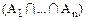Покажем несколько применений принципа включения и исключения

Теорема 2. Пусть |X|=n, |Y|=k, то число всех функций f:X®Y и f(X)=Y, равно

S _n,k=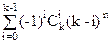

Доказательство

Пусть У={y₁,…,y_k} и A_i={f: f:X®Y & y_iÏf(X)}, тогда

f(X)¹YÛfÎ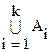

Множество всех f:X®Y имеет мощность kⁿ. Определим 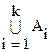, пусть 1£p₁£…£p_i£k пересечение 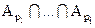есть множество всех функций f:X®Y таких, 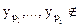f(X), a, следовательно, мощность этого пересечения ровно (m-i)ⁿ. Согласно теоремы 1 имеем

S _n,k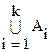=kⁿ-||=kⁿ-=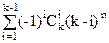

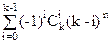
Эта формула дает простое выражение для вычисления чисел Стирлинга 2^го рода

S(n,k)=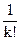 S _n,k=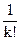

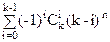
Рассмотрим вопрос об определении числа “беспорядков” на множестве {1,…,n}

Определение. Под беспорядком на множестве {1,…,n} будем понимать произвольную перестановку f этого множества, такую что f(i)¹i для 1£i£n.

Пусть D_n – множество всех беспорядков на {1,…,n} и

A_i={fÎS_n: f(i)=i}, i=1,…,n.

Заметим, что fÎD_n ÛfÏ A_i для "iÎ{1,…,n}, следовательно

|D_n|=|S_n|-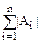+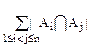-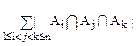+…(-1)^n-1||

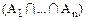Для произвольной последовательности 1£p₁£…£p_i£n пересечение 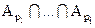является множеством таких перестановок f, для которых f(p_j)=p_j для 1£j£n, и значит, |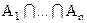|=(n-i)!. Заметив, что последовательность 1£p₁£…£p_i£n можно выбрать 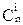способами, получаем в итоге

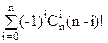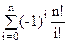|D_n|== =n!()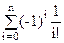

Отметим, что сумма в скобках является начальным членом ряда е^-1=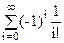. Это означает, что беспорядки составляют е^-1=0.36788… всех перестановок.

Перечисление графов [5]

Дата добавления: 2014-01-06