Композиции чисел

Теорема 8. Пусть C(m,n) обозначает число композиций числа n точно с m частями, тогда C(m,n)=.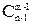

Доказательство 1.

Рассуждение, используемое в доказательстве теоремы 4, можно легко применить для доказательства того, что

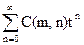= (t¹+ t²+ t³+ t⁴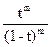+…)^m==t^m==.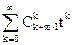

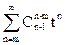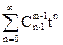Приравнивая коэффициенты при tⁿ в крайних членах этой цепочки равенств, получаем требуемое.

Доказательство 2.

Введем графическое представление для композиций числа n. C композицией (a₁a₂…a_m) числа n связываем m сегментов интервала [0, n]; первый сегмент имеет длину а₁, второй – длину а₂ и т. д. Например, композиция (3 2 3 1 2) числа 11 представим в виде

0←1─2→3←4→5←6─7→8↔9←10→11

Заметим теперь, что можно построить каждую из С(m,n) композиций числа n c m частями, выбирая m-1 чисел из n-1 первых целых как конечные точки для таких m сегментов, разделяющих интервал [0, n]. Поскольку таких выборов может быть 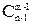, видим, что C(m,n)=.

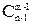Простота теоремы 6 позволяет получать чисто асимптотические выражения для некоторых функций разбиений, связывая их с функциями композиций. Например,

Теорема 9. (Эрдеш – Ленер). Пусть Р_M(n) обозначает число разбиений числа n ровно с М частями, тогда при n→∞

Р_M(n)≈ 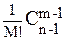, если M=o(n^1/3).

Задачи

1.Пусть F_n – n-е число Фибоначчи F₀=0, F₁=1, F_n=F_n-1+F_n-2, n>1. Показать, что число композиций n, в которых нет единиц, равно F_n-1.

2. В более общем виде – Пусть kF_n – определяется по правилу;

kF₀=…=kF_k-2, kF_k-1=1, kF_n=kF_n-1+kF_n-k.

Показать, что число композиций n, в которых все части ≥ k, равно kF_n-1.

3. Из задачи 2 следует, имеется 2^n-1 композиций числа n.

4. пусть С_k(m,n) обозначает число композиций n точно с m частями, каждая из которых не меньше k. Тогда

С_k(m,n)=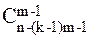

5. Из задач 2 и 4 следует, что

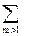
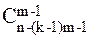= kF_n-1

Дата добавления: 2014-01-06