Основная лемма

Пусть G – конечная группа. Предположим, элементы G ведут себя, как подстановки множества S; это значит, что существует отображение G в симметрическую группу множества S. Другими словами gÎG мы поставим в соответствие подстановку множества S, которую обозначим через p_g. Предположим, что это отображение – гомоморфизм, т. е.

p_gg¢=p_g×p_g¢ (6)

для всех gÎG, g¢ÎG. Заметим, что различные элементы G не обязательно соответствуют различным подстановкам.

В нашем случае G порождает отношение эквивалентности на элементах множества S. Два элемента s₁, s₂ множества S называются эквивалентными, записывается s₁~s₂, если существует gÎG, такой что p_gs₁~s₂. В самом деле:

1. s~s, для всех sÎS [так как формула (6) показывает, что если e – единичный элемент группы G, то p_е – тождественная подстановка, т. е. оставляющая на месте все точки S].

2. Если s₁~s₂, то s₂~s₁ [так как формула (6) показывает, что если g¢=g^-1, то, ×p_g¢=(p_g)^-1].

3. Если s₁~s₂, s₂~s₃ то s₁~s₃ [так как если p_gs₁~s₂, p_g¢s₂~s₃, то p_g¢×g s₁= p_g¢(p_g s₁)= p_g¢(s₂)=s₃].

В нашем случае классы эквивалентности называют транзитивными множествами.

Лемма 1. Число транзитивных классов множества равно

,

где ½G½обозначает число элементов в группе G и для каждого g y(g) обозначает число элементов множество S, остающихся инвариантными при подстановках p_g, т.е. число элементов sÎS, для которых p_gs=s.

Доказательство.

Рассмотрим все пары (g,s), для которых gÎG, sÎS, p_gs=s. Число n таких пар может быть вычислено двумя способами. Во-первых, для каждого фиксированного g можно подсчитать число элементов s, удовлетворяющих условию p_gs=s, отсюда число пар

n=.

С другой стороны, для каждого sÎS можно подсчитать число элементов g со свойством p_gs=s. Обозначив это число через h(s), получим

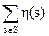=. (7)

Для фиксированного s элементы группы G, обладающие свойством p_gs=s, образуют подгруппу группы G, которую обозначим через G_s. Порядок этой группы равен h(s).

Если s_i эквивалентно s, то число элементов g, таких, что p_gs=s_i равно½G_s½. Это следует из того, что существует элемент hÎG, удовлетворяющий условию p_hs₁=s, а теперь равенство p_gs=s₁ означает то же самое, что и hgÎG_s. Таким образом, если s₁ и s фиксированы, то число возможностей для g равно как раз числу элементов в G_s.

Соответственно G может быть разбита на подмножества, каждое из которых состоит из ½G_s½элементов и соответствует ровно одному элементу того класса эквивалентности, в который входит s. Отсюда следует, что этот класс эквивалентности содержит ½G½/½G_s½элементов. Поэтому имеем

h(s)=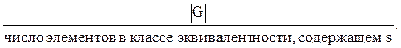

Суммируя по s, получаем, что сумма чисел h(s) для всех s, принадлежащих одному и тому же классу эквивалентности, равны½G½. Следовательно, сумма всех h(s) равна взятому ½G½раз числу классов эквивалентности, т.е. формула (7) доказывает лемму.

Дата добавления: 2014-01-06