Перевод чисел из одной системы счисления в другую

Перевод целого числа из десятичной системы в любую другую позиционную систему счисления

Назовем старую систему, т.е. систему из которой выполняется перевод Р-ичной, а систему в которую он выполняется Q-ичной.

При переводе целого десятичного числа в систему с основанием q его необходимо последовательно делить на q до тех пор, пока не останется остаток, меньший или равный q– 1. Число в системе с основанием q записывается как последовательность остатков от деления, записанных в обратном порядке, начиная с последнего.

Пример: Перевести число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

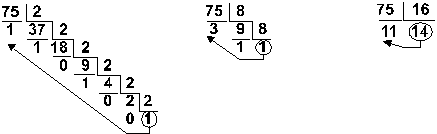
Ответ: 75₁₀ = 1 001 011₂ = 113₈ = 4B₁₆.

Перевод правильной десятичной дроби в любую другую позиционную систему счисления

Пpи переводе правильной десятичной дpоби в систему счисления с основанием q необходимо сначала саму дробь, а затем дробные части всех последующих произведений последовательно умножать на q, отделяя после каждого умножения целую часть произведения. Число в новой системе счисления записывается как последовательность полученных целых частей произведения.

Умножение производится до тех поp, пока дробная часть произведения не станет равной нулю. Это значит, что сделан точный перевод. В противном случае перевод осуществляется до заданной точности. Достаточно того количества цифр в результате, которое поместится в ячейку.

Пример: Перевести число 0,35 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:

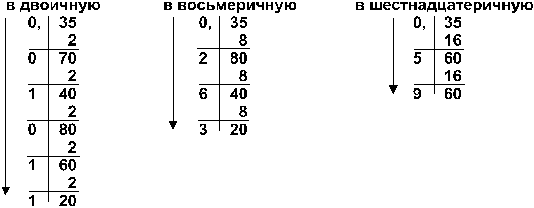
Ответ: 0,35₁₀ = 0,01011₂ = 0,263₈ = 0,59₁₆.

Перевод неправильной десятичной дроби в любую другую позиционную систему счисления

Общая методика:

- представить Р-ичное число двумя операндами, т.е. в виде целой и дробной части (правильной дроби);

- произвести перевод каждого из операндов в новую Q-ичную систему по конкретным правилам;

- сформировать представление числа в новой Q-ичной системе, записав через разделитель полученное изображение целой и дробной части.

Примеры: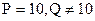

1. 47,4₁₀ перевести в двоичную систему.

2. Преобразовать 47,4₁₀ в восьмеричную систему.

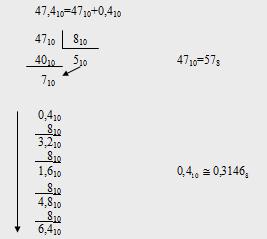
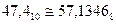
Пример 3: 47,4₁₀ преобразовать в шестнадцатеричную систему.

47,4₁₀=47₁₀+0,4₁₀

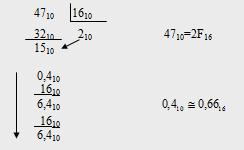
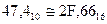
Анализ рассмотренных примеров позволяет сделать выводы:

- чем меньше основание новой системы счисления, тем больше разрядов в изображении числа;

- перевод чисел из десятичной системы в двоичную требует выполнения значительного количества действий (удобнее перевести десятичное число сначала в восьмеричное или шестнадцатеричное, а затем перейти к двоичному числу с использованием триад или тетрад);

- чем больше основание системы по отношению к десяти, тем менее удобно оно для человека.

Перевод числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную

При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Примеpы:

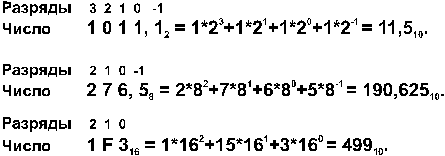
Примеры обратных переводов чисел, т.е. из системы с 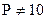в систему Q=10:

Пример 1:

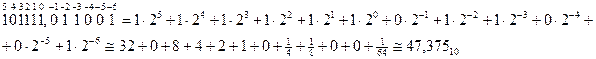
Пример 2: 2F,66₁₆ преобразовать в десятичную систему.

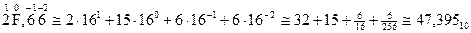
Анализ полученного результата позволяет сделать вывод, что истинное значение в новой десятичной системе счисления получить не удается, результат есть приближенное уменьшенное значение, причем количество разрядов в дробной части исходного числа определяет степень погрешности результата. Чем разрядов больше, тем погрешность меньше.

Перевод числа из восьмеричной, шестнадцатеричной системы в двоичную и наоборот

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр). Например:

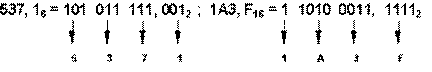
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой. Например,

Дата добавления: 2014-01-06