
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аксиомы и законы алгебры логики
|
|
|
|
Как и обычная алгебра, булева алгебра содержит ряд фундаментальных правил, которые принимаются без доказательства и называются аксиомами. Аксиомы служат основой для доказательства теорем, являющихся законами булевой алгебры. Аксиомы и законы используются для упрощения булевых функций.
Аксиомы алгебры логики
| Номер аксиомы | Формулировка | Пояснения |
| A1 | x=0, если x¹1 | Булева переменная всегда равна нулю либо единице |
| A2 | x=1, если x¹0 | |
| A3 | x=0, если 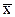 =1 =1
| Инверсное значение переменной x противоположно ее прямому значению |
| A4 | x=1, если 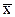 =0 =0
| |
| A5 | 0×0=0 | Правила выполнения логического умножения (конъюнкции) |
| A6 | 1×1=1 | |
| A7 | 0×1=1×0=0 | |
| A8 | 0Ú0=0 | Правила выполнения логического сложения (дизъюнкции) |
| A9 | 1Ú1=1 | |
| A10 | 0Ú1=1Ú0=1 |
Полученная система аксиом непосредственно следует из определения функций НЕ, И и ИЛИ.
Теоремы алгебры логики
| № | Формулировка | Пояснения |
| 1. Идентичность | ||
| T1 | x Ú 0 = x | Доказательство теоремы T1 следует из аксиом A8 и A10, в которых первое слагаемое заменено на x. Теорема T1 говорит, что из булева выражения можно удалить часть, равную нулю и связанную с остальным выражением операцией дизъюнкция. |
| T2 | x × 1 = x | Теорема T2 доказывается на основе аксиом A6 и A7 и говорит, что из булева выражения можно удалить часть, равную единице и связанную с остальным выражением операцией конъюнкция. |
| 2. Наличие нулевых элементов | ||
| T3 | x Ú 1 = 1 | Теорема T3 следует из A9 и A10, свидетельствуя о том, что если какая-то часть булева выражения, связанная с остальным выражением операцией дизъюнкция, равна единице, то и все выражение равно единице. |
| T4 | x × 0 = 0 | Теорема T4 следует из A5 и A5, свидетельствуя о том, что если какая-то часть булева выражения, связанная с остальным выражением операцией конъюнкция, равна нулю, то и все выражение равно нулю. |
| 3. Идемпотентность | ||
| T5 | x Ú x = x x Ú x Ú...Ú x = x | Теорема T5 следует из A5 и A9 и свидетельствует, что добавление или удаление идентичных частей булева выражения, связанных операцией дизъюнкция с остальной частью выражения, не меняет значения булева выражения. |
| T6 | x × x ×... × x = x | Теорема T6 следует из A5 и A6 и свидетельствует о том, что умножение булева выражения на само себя не меняет значения булева выражения. |
| 4. Эволюция (двойное отрицание) | ||
| T7 | 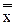 = x = x
| Теорема T7 доказывается последовательным применением аксиом A3 и A4. Из T7 следует, что двойное отрицание булева выражения не меняет его значения. Таким образом, любое четное число отрицаний булева выражения может быть введено или удалено без изменения значения выражения. |
| 5. Дополняемость | ||
| T8 | x Ú 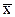 = 1 = 1
| Дизъюнкция двух взаимообратных выражений всегда равна единице независимо от значений выражений. Если x=0, то 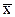 =1 и xÚ =1 и xÚ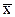 =0Ú1=1; если x=1, то =0Ú1=1; если x=1, то 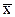 =0 и xÚ =0 и xÚ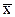 =1Ú0=1. =1Ú0=1.
|
| T9 | x × 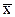 = 0 = 0
| Конъюнкция двух взаимообратных выражений всегда равна нулю независимо от значений выражений. Если x=0, то 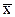 =1 и x& =1 и x&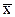 =0&1=0; если x=1, то =0&1=0; если x=1, то 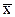 =0 и xÚ =0 и xÚ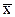 =1&0=0. =1&0=0.
|
| 6. Ассоциативность | ||
| T10 | (aÚb)Úc = aÚ(bÚc) | Теоремы T10 и T11 аналогичны теоремам обычной алгебры и свидетельствуют о том, что значение булева выражения не зависит от порядка вычисления значений его частей. |
| T11 | (a×b)×c = a×(b×c) | |
| 7. Коммутативность | ||
| T12 | a Ú b = b Ú a | Теоремы T12 и T13 свидетельствуют о том, что перестановка членов булева выражения не меняет его значения. Эти теоремы аналогичны теоремам обычной алгебры. |
| T13 | a × b = b × a | |
| 8. Дистрибутивность | ||
| T14 | a×b Ú a×c = a×(bÚc) | Теорема T14 представляет собой процесс вынесения общей переменной за скобки. |
| T15 | (aÚb)×(aÚc) = a Ú b×c | Теорема T15 не имеет своего аналога в обычной алгебре, но ее справедливость может быть доказана на основе рассмотренных выше аксиом и теорем. |
| 9. Поглощение | ||
| T16 | a Ú a×b = a | Теоремы T16 и T17 позволяют уменьшить число членов булева выражения. |
| T17 | a×(aÚb) = a | |
| 10. Склеивание | ||
| T18 | a×b Ú a×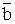 = a = a
| Теоремы T18 и T19 также позволяют уменьшить число членов булева выражения. |
| T19 | (aÚb) × (aÚ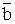 ) = a ) = a
| |
| 11. Законы Де Моргана | ||
| T20 | 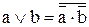
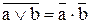
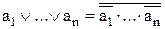
| Теоремы Де Моргана имеют важнейшее значение в алгебре логики. Их суть заключается в замене одной операции на другую: операции дизъюнкция на операцию конъюнкция, или наоборот. Понятно, что просто так подобную замену сделать нельзя, поскольку операции совершенно разные и результирующее выражение будет отличаться от исходного. Поэтому для сохранения эквивалентности выражений после замены одной операции на другую над каждым элементом выражения должна быть поставлена инверсия, и над всем выражением также должна быть поставлена инверсия. |
| T21 | 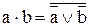
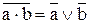

|
Лекция 11
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 4785; Нарушение авторских прав?; Мы поможем в написании вашей работы!