Аналитическое представление функций алгебры логики

Мы уже познакомились с представлением произвольной булевой функции в виде таблицы истинности. Табличное представление является наиболее наглядным и наиболее просто формируется. В то же время оно является громоздким и не позволяет компактно представить булеву функцию.

Рассмотрим две канонические формы аналитического представления булевых функций. В их основе лежит понятие булева терма.

Терм – это выражение, связывающее переменные или их инверсии одной операцией. В качестве связывающей операции обычно выступает конъюнкция или дизъюнкция. Рангом терма называется количество переменных в терме.

Конъюнктивный терм (например, 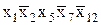) называют иногда словом минтерм, поскольку он принимает единичное значение только лишь в одном случае: когда x₁=1, x₂=0, x₅=1, x₇=0, x₁₂=0. При любых других значениях переменных значение терма будет равно нулю. Минимальное количество ситуаций, когда терм равен единице (собственно, лишь одна такая ситуация) и определяет его название – минтерм.

Дизъюнктивный терм (например, 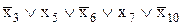) называют также словом макстерм. Терм равен единице во всех случаях, кроме одного: если x₃=1, x₅=0, x₆=1, x₇=0, x₁₀=1, то терм равен нулю. То есть дизъюнктивный терм равен единице в максимально возможном количестве случаев, поэтому и называется макстерм.

Дизъюнктивная нормальная форма (ДНФ)

Дизъюнктивной нормальной формой (ДНФ) называется функция алгебры логики, представленная в виде набора конъюнктивных термов (минтермов), связанных операцией дизъюнкции. Примерами ДНФ являются следующие выражения:

;

;

;

;

.

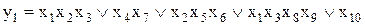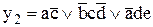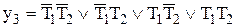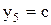Рассмотрим на примере процесс построения ДНФ функции, заданной таблицей истинности. Пусть некоторая булева функция задана следующей таблицей истинности:

x1	x2	x3	f

Рассмотрим строки таблицы, равные единице. Во второй строке таблицы функция равна единице при условии x₁=0, x₂=0, x₃=1. Единичному значению функции f(x₁=0, x₂=0, x₃=1) будет соответствовать минтерм 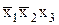, поскольку он равен единице только при данных значениях аргументов. Остальным строкам таблицы, в которых f=1, будут соответствовать следующие минтермы: 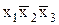, , 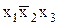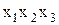. Поскольку наша функция равна единице на втором наборе аргументов ИЛИ на пятом наборе ИЛИ на шестом наборе ИЛИ на восьмом наборе, то для получения окончательной аналитической записи нашей функции полученные нами минтермы следует объединить операцией ИЛИ. В результате получим следующую ДНФ:

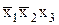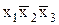f = Ú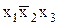ÚÚ.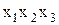

По сути, каждый терм здесь отвечает за определенную строку таблицы истинности, то есть за одну из ситуаций, когда функция принимает единичное значение. Если, например, все аргументы функции будут равны нулям (первая строка таблицы истинности), то в построенной ДНФ каждый из четырех термов будет равен нулю, и их дизъюнкция также будет равна нулю. Таким образом, функция даст нулевое значение, что совпадает с ее таблицей истинности.

Отметим, что если в ДНФ ранг каждого терма равен количеству аргументов функции, то такая формула называется совершенной дизъюнктивной нормальной формой или СДНФ. Наша функция f, а также функции y₃, y₄, y₅ на предыдущей странице, представлены в виде СДНФ.

Таким образом, алгоритм построения СДНФ по таблице истинности заключается в следующем:

1. Для каждой строки таблицы истинности, равной единице, сформировать минтерм, в котором аргументы, равные нулю, указать с инверсией, а аргументы, равные единице, указать без инверсии.

2. Объединить все полученные термы операцией дизъюнкция.

Конъюнктивная нормальная форма (ДНФ)

Конъюнктивной нормальной формой (КНФ) называется функция алгебры логики, представленная в виде набора дизъюнктивных термов (макстермов), связанных операцией конъюнкции. Примерами КНФ являются следующие выражения:

;

;

;

;

.

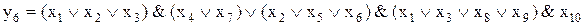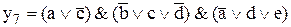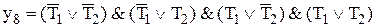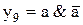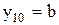Поскольку операция конъюнкции имеет более высокий приоритет по сравнению с операцией дизъюнкции, то макстермы, содержащие более одной переменной, обязательно должны заключаться в скобки.

Рассмотрим на примере процесс построения КНФ функции, заданной таблицей истинности. Пусть некоторая булева функция задана следующей таблицей истинности:

x1	x2	x3	f

Рассмотрим строки таблицы, равные нулю. В первой строке таблицы функция равна нулю при условии x₁=0, x₂=0, x₃=0. Нулевому значению функции f(x₁=0, x₂=0, x₃=0) будет соответствовать макстерм 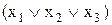, поскольку он равен нулю только при данных значениях аргументов. Остальным строкам таблицы, в которых f=0, будут соответствовать следующие макстермы: 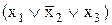, , 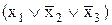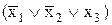. Поскольку наша функция равна нулю на первом наборе аргументов И на третьем наборе И на четвертом наборе И на седьмом наборе, то для получения окончательной аналитической записи нашей функции полученные нами макстермы следует объединить операцией И. В результате получим следующую КНФ:

f = &&&.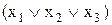

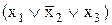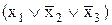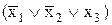В формуле КНФ каждый терм отвечает за определенную строку таблицы истинности, то есть за одну из ситуаций, когда функция принимает нулевое значение. Если, например, все аргументы функции будут равны единицам (последняя строка таблицы истинности), то в построенной КНФ каждый из четырех термов будет равен единице, и их конъюнкция также будет равна единице. Таким образом, функция даст единичное значение, что совпадает с ее таблицей истинности.

Отметим, что если в КНФ ранг каждого терма равен количеству аргументов функции, то такая формула называется совершенной конъюнктивной нормальной формой или СКНФ. Наша функция f, а также функции y₈, y₉, y₁₀ на предыдущей странице, представлены в виде СКНФ.

Таким образом, алгоритм построения СКНФ по таблице истинности заключается в следующем:

1. Для каждой строки таблицы истинности, равной нулю, сформировать макстерм, в котором аргументы, равные единице, указать с инверсией, а аргументы, равные нулю, указать без инверсии.

2. Объединить все полученные термы операцией конъюнкция.

Отметим следующее. В наших примерах мы строили СДНФ и СКНФ по одной и той же таблице истинности. Хотя внешне полученные СДНФ и СКНФ совершенно не похожи между собой, они представляют аналитические записи одной и той же булевой функции, то есть оба выражения полностью эквивалентны. Подставляя любой из наборов аргументов в СДНФ, мы получим то же самое значение, что и с помощью СКНФ для того же набора аргументов. СДНФ и СКНФ являются аналитической записью содержимого таблицы истинности будевой функции.

Может показаться, что полученные нами СДНФ и СКНФ достаточно громоздки и сложны, и гораздо проще пользоваться таблицей истинности. Причина в том, что таблица истинности функции f была составлена таким образом, чтобы количество наборов, при которых функция равна единице, и наборов, при которых функция равна нулю, выбрано одинаковым. В общем случае количество единичных и нулевых строк будет различным.

Рассмотрим, например, следующую таблицу истинности (к слову, это таблица функции конъюнкции от трех аргументов). Данная функция принимает единичное значение лишь на одном наборе из восьми, а нулевое – на семи наборах. СКНФ и СДНФ будут иметь следующий вид:

СДНФ(f_И) = .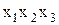

СКНФ(f_И) = &&&&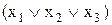

&&&

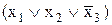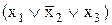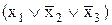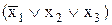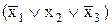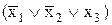
x1	x2	x3	fИ

Очевидно, что СДНФ получилась значительно короче, чем СКНФ, хотя и является ее эквивалентом. Это связано с тем, что СДНФ учитывает только строки, в которых функция равна единице, а СКНФ – строки, в которых функция равна нулю. Представление такой функции в виде СДНФ предпочтительнее, чем виде СКНФ или таблицы истинности.

Рассмотрим следующую таблицу истинности (таблицу истинности операции ИЛИ от трех аргументов):

x1	x2	x3	fИЛИ

СДНФ и СКНФ в этом случае будут следующими:

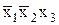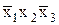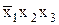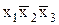СДНФ(f_ИЛИ) = ÚÚ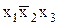ÚÚ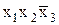ÚÚ.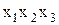

СКНФ(f_ИЛИ) = .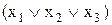

В данном случае более короткая запись у СКНФ, поскольку в таблице истинности строка, в которой функция равна нулю, только одна, а строк, в которых функция равна единице, семь.

Таким образом, можно сформулировать следующее правило: если в таблице истинности количество строк, в которых f=0, превышает количество строк, в которых f=1, то более кратким будет представление функции в виде СДНФ. В противном случае более кратким будет представление функции в виде СКНФ.

Пусть, например, некоторая функция задана в виде следующей СДНФ:

y = 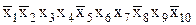Ú.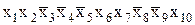

Что можно сказать об этой функции? Очевидно, что функция зависит от десяти аргументов x₁-x₁₀, и ее СДНФ состоит из двух термов. Это означает, что функция принимает единичное значение только лишь в двух строках таблицы истинности, соответствующих данным термам. В остальных строках функция равна нулю.

Сколько же всего строк в таблице истинности? Поскольку функция зависит от десяти переменных-аргументов, то число строк в таблице истинности (число различных вариантов наборов аргументов) будет равно 2¹⁰=1024. Следовательно, в 1022 случаях функция принимает нулевое значение, и лишь в двух – единичное. Если бы мы попытались записать ее в виде СКНФ, нам потребовалось бы 1022 макстерма, что заняло бы несколько страниц текста и несколько часов времени. Понятно, что запись такой функции в виде СДНФ значительно более компактна по сравнению с СКНФ или таблицей истинности.

Можно привести и противоположный пример. Пусть булева функция задана следующей СКНФ:

y = &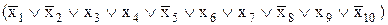

&.

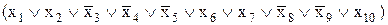Очевидно, что перед нами булева функция десяти переменных, равная нулю в 2 случаях из 1024. В оставшихся 1022 случаях функция равна единице, и ее СДНФ будет состоять из 1022 минтермов. Запись подобной функции в виде СКНФ значительно более компактна по сравнению с СДНФ или таблицей истинности.

Необходимо подчеркнуть, что даже если в таблице истинности количество единичных строк превышает количество нулевых строк, то запись функции в виде СДНФ не будет ошибочной. Она будет менее компактной по сравнению с СКНФ, но ошибочной не будет. Необходимо помнить, что правильно составленные СДНФ и СКНФ при всем своем внешнем различии являются полностью эквивалентными (тождественными). Поскольку СДНФ более проста в построении, то часто булевы функции записывают именно в дизъюнктивной форме.

Лекция 12

Дата добавления: 2014-01-06