Модель фона в приближении теплового источника

Пусть для фона справедливы приближения теплового источника. К этому типу фоновых образований можно отнести распределение яркости излучения сельских, городских и др. ландшафтов в среднем и дальнем ИК диапазонах длин волн. В этом случае распределение флуктуаций яркости обусловлено флуктуациями пространственного распределения температуры. Если амплитуда температурных флуктуаций невелика по сравнению со значением среднего уровня температуры фона , то, без существенной потери точности, математические выражения, описывающие флуктуации яркости фона, можно представить функциями с разделяющимися переменными, а именно,

(1.15)

где

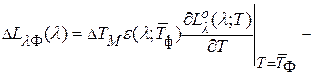(1.16)

-функция, описывающая распределение по длинам волн флуктуаций яркости;

(1.17)

- функция, описывающая нормированное пространственное распределение флуктуаций температуры фона относительно среднего уровня в пределах наблюдаемой области пространства предметов , причём

(1.18)

- максимальное значение флуктуаций температуры в пределах области пространства .

Как следует из анализа формул (1.15) и (1.16), зависимость флуктуаций яркости теплового фона от длины волны 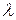носит регулярный характер. При заданном значении средней температуры фона реализации в первом приближении определяются функцией контрастной яркости АЧТ, коэффициентом спектральной излучательной способности, усредненным по пространственным координатам, а также величиной флуктуаций температурного перепада 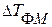. Поэтому статистические свойства флуктуаций спектральной яркости теплового фона можно описать одномерной плотностью вероятности , в которой 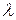рассматривается как параметр.

Так как при сделанных допущениях флуктуации яркости линейно зависят от флуктуаций температуры, то конкретный вид функции однозначно определяется функцией плотности вероятности значений флуктуаций температуры .

Если флуктуации температуры распределены, например, по гауссовскому закону, то одномерная плотность вероятности амплитуды спектральной яркости также гауссовская и имеет вид

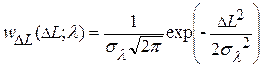, (1.19)

где

(1.20)

- среднеквадратическое отклонение флуктуаций яркости фона на длине волны ;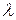

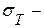среднеквадратическое отклонение флуктуаций температуры фона.

Тогда в рамках корреляционной теории реализации сигнала в виде флуктуаций спектрального распределения яркости теплового фона можно характеризовать корреляционной функцией вида

, (1.21)

где 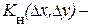нормированная ковариационная функция, описывающая пространственные флуктуации случайного стационарного поля яркости.

Выведенное соотношение (1.21) для случайного теплового фона подтверждает предположение, сделанное В.Л.Лёвшиным [30], о возможности представления ковариационной функции фона, как функции с разделяющимися переменными.

На основе экспериментальных исследований наземных аэроландшафтов установлено, что для изотропных фоновых образований можно использовать аппроксимацию нормированной ковариационной функции функцией вида [13]

, (1.22)

где

(1.23)

- угловая координата, измеряемая обычно в миллирадианах (мрад);

дальность до предметной плоскости;

коэффициент аппроксимации;

коэффициент аппроксимации, имеющий смысл эффективной пространственной частоты и измеряемый в мрад^-1.

Если распределение поля флуктуаций яркости фона не является изотропным, то нормированную ковариационную функцию можно аппроксимировать функцией вида

, (1.24)

где и 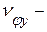коэффициенты аппроксимации, имеющие смысл эффективных пространственных частот в направлении координатных осей и , соответственно.

Важно отметить, что в рамках предложенной выше модели излучения фонов, как тепловых источников, для большинства типовых ландшафтов, вид функций (1.22), (1.24) и соответствующих коэффициентов аппроксимации можно считать инвариантными, по крайней мере, в пределах суточного интервала. Это обусловлено тем, что при колебаниях температуры, в основном, изменяется среднеквадратическое отклонение спектральной яркости .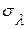

Вид функции 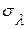, описывающей распределение спектральной яркости флуктуаций теплового фона, не сложно рассчитать, используя формулу (1.20), если априори известны пределы флуктуаций температуры. Например, для гауссовского закона распределения флуктуаций температуры в пределах от 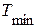до , среднеквадратическое отклонение (СКО) флуктуаций яркости 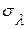рассчитывается по формуле (1.20) при , равном

. (1.25)

Для бинарного закона

. (1.26)

Следует отметить, что бинарный закон достаточно хорошо описывает распределение значений яркости для такого типа фона, как облачное небо [13]. При этом нормированная корреляционная функция может быть аппроксимирована зависимостью вида

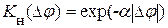. (1.27)

Если приближения теплового источника для фоновых образований не выполняются, как, например, в видимом или ближнем ИК диапазонах длин волн, то для построения математических моделей, требуется учитывать не только распределение температуры по поверхности, определяющее распределение яркости собственного излучения, но также распределение яркости отраженного излучения от внешних источников. Описание распределения яркости отраженного излучения требуется делать с учетом возникающего при внешней подсветке эффекта затенения. Поэтому математические модели, учитывающие пространственное распределение излучения фонов в видимом и ближнем диапазонах длин волн, строят, в основном, на основе данных экспериментальных исследований.

Наиболее сложной задачей является описание фоновых образований, содержащих границы раздела типовых фоновых ансамблей. В качестве примера, можно указать ансамбли реализаций фона, содержащих небесную сферу, отделенную линией горизонта от подстилающей поверхности суши или воды. Другим примером могут быть ансамбли реализаций в виде аэроландшафтов, содержащих как водную, так и земную поверхности, разделенные прибрежной зоной. Следует иметь в виду, что перечисленные типы фонов наиболее неблагоприятны для задач пеленгации объектов [30], т.к. пространственные спектры их реализаций содержат составляющие в широком диапазоне частот.

Характерной особенностью таких фонов является бимодальность одномерных плотностей вероятности распределения значений яркости. Логично предположить, что бимодальность является следствием неоднородности случайных полей данного типа. По этой причине для модельного описания этих фонов нельзя использовать корреляционную теорию. В [30] для оценки помехозащищенности пеленгационных ОЭП при наличия в поле анализа подобных фоновых образований предлагается использовать модель в виде «ступени».

Если граница скачкообразного перехода между двумя различными уровнями спектральной яркости и считается прямолинейной и расположенной вдоль координатной оси , то

. (1.28)

Уровни спектральной яркости и определяются, как математические ожидания спектрального распределения яркости в соответствующих областях по обе стороны от границы раздела.

Модельное описание сигналов от объектов и фоновых образований не может быть полным, т.к. практически всегда вероятностная модель физических процессов, порождающих такие сигналы, неизвестна или известна не полностью. Это вынуждает проектанта принимать допущения относительно свойств источников сигналов, доопределяющие модельное описание фонов, или решать задачу проектирования в условиях априорной статистической неопределенности.

Дата добавления: 2014-01-06