Математические модели излучения фонов

ЛЕКЦИЯ 5

Реализации сигналов от фоновых образований представляют собою случайные поля, которые описываются в терминах яркости излучения многомерными случайными функциями вида 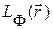, определенными в координатном пространстве 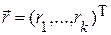. В большинстве практически интересных случаев фоновые случайные поля удобно рассматривать как флуктуации спектральной яркости излучения 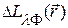относительно значения математического ожидания 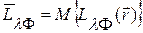распределения яркости, т.е.

Очевидно, что фоновые поля могут существенно отличаться по своим свойствам, как, например, фон, образованный звёздным небом, и аэроланшафт подстилающей лесной местности. Тем не менее, множество фоновых полей можно разделить на типы таким образом, что любую из реализаций можно отнести к определенному ансамблю случайных полей , каждый из которых характеризуется многомерной плотностью вероятности .

На функционально-логическом уровне математическая модель фона, как источника оптического сигнала, представляется в виде множества 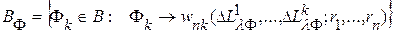реализаций типовых ансамблей 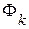фона.

Описание реально существующих фоновых полей в таком виде при условии, что их реализации являются функциями многих аргументов, а размерность плотности вероятности ничем не ограничена, связано с практически непреодолимыми трудностями. Поэтому обычно делают ряд допущений, существенно упрощающих проблему математического моделирования фоновых полей.

Во-первых, будем рассматривать фоновые поля как статические, пренебрегая возможной зависимостью распределения реализаций яркости фона от времени, и ламбертовские, т.е. имеющие одинаковую яркость по направлениям распространения излучения.

При сделанных допущениях реализации фоновых полей описываются функциями трех переменных . В некоторых частных случаях, которые будут рассмотрены ниже, функции можно представить функциями с разделяющимися переменными. Представление флуктуаций яркости фона в таком виде существенно упрощает задачу математического моделирования фоновых полей. Но, к сожалению, такое допущение не всегда оправдано.

Во-вторых, фоновые образования можно разделить на ряд типовых случайных полей, которые с некоторой степенью приближения обладают свойствами таких наиболее изученных случайных процессов, как гауссовские и марковские. Удобство такого описания заключается в том, что мерные плотности вероятности для этих случайных процессов выражаются через двумерные плотности вероятности [Тихонов В.И.].

В третьих, принимается допущение о том, что фоновые образования являются однородными в широком смысле случайными полями, т.е. их математические ожидания не зависят от координат пространства, а корреляционная функция является функцией только разности аргументов, а именно .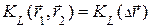

Примечание:

Реализации случайных сигналов описывают случайными функциями, образующими некоторый ансамбль с присущими этому ансамблю свойствами. Свойства ансамбля характеризуют функциями, которые получаются путем усреднения по ансамблю. Для неоднородного случайного поля светимости или яркости используют для описания свойств корреляционные функции:

;

,

где оператор вычисления математического ожидания.

Для однородного случайного поля светимости или яркости используют для описания свойств корреляционные функции, имеющие вид 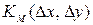,, или спектральные функции, которые вычисляются как преобразование Фурье от соответствующих корреляционных функций, , .

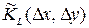При таком допущении можно строить математические модели фона в рамках корреляционной теории. Согласно этой теории случайные поля характеризуются математическим ожиданием и ковариационной функцией. Корреляционная теория абсолютно справедлива для однородных гауссовских и марковских случайных процессов и полей, многомерные плотности вероятности которых, как отмечалось ранее, выражаются через соответствующие двумерные плотности вероятности.

Несмотря на кажущуюся ограниченность применения корреляционной теории, в большинстве практически интересных случаев математическое моделирование фоновых образований осуществляют на основе именно этой теории. Главным образом, это оправдывается ограниченностью возможностей получения экспериментальных данных о многомерной статистике фона. Поэтому, даже экономически целесообразно интерполировать закон распределения на основе экспериментально полученной корреляционной функции и в качестве первого приближения пользоваться нормальным законом.

Рассмотрим теперь математические модели типичных фоновых образований при сделанных выше допущениях.

Дата добавления: 2014-01-06