Протяжённый сигнал

Вид тестовых сигналов

Для выполнения процедур проектирования (анализа, синтеза и оптимизации) необходимо использовать модели тестовых сигналы. Рассмотрим типы таких тестовых сигналов.

Такие тестовые сигналы используются при оценке пороговой чувствительности ОЭП, например, пороговой разности температур 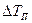. Сигнал имеет вид резкого перепада.

, (14)

где 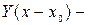функция Хэвисайда.

2) Точечный сигнал

, (15)

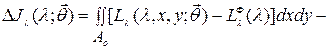где (16)

- спектральная сила излучения объекта.

Модель точечного источника используется в тех ситуациях, когда угловой размер объекта во много раз меньше углового размера 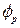пятна рассеяния, т.е. .

3) Финитный сигнал

Очевидно, что для целей проектирования подход, основанный на использовании моделей источников оптических сигналов, имитирующих сколь угодно близко свойства реальных объектов, не годится, т.к. он избыточен и требует значительных ресурсов вычислительной техники и временных затрат. Чтобы обойти проблемы, связанные с избыточностью описания тестовых сигналов, предлагается в качестве тестовых выбирать такие сигналы, которые образуют базис функционального преобразования сигналов, осуществляемого в тракте ОЭП на этапе, предшествующем формированию решающей статистики. Рассмотрим подробно этот вопрос.

Как дискретную выборку, так и аналоговый сигнал можно представить разложением в ортогональном базисе. В первом случае базисными являются функции последовательных отсчетов, а во втором случае в качестве базисных обычно используют системы ортогональных функций Фурье, Бесселя, Уолша, Адамара, Карунена-Лоева и др. [13, 14].

В подавляющем большинстве случаев достаточным описанием сигналов является представление его в виде линейной суперпозиции ограниченного числа ортогональных базисных функций 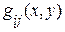, а именно,

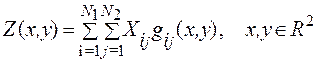. (16а)

Следовательно, в качестве тестовых можно использовать сигналы, которые описываются как отдельные слагаемые разложения (1.71). Количество тестовых сигналов ограничивается размерностью выборки, используемой в алгоритме анализа реализаций. При моделировании ОЭП, предназначенных для обнаружения и оценки параметров сигналов, может оказаться достаточным использование тестового сигнала, описываемого одним членом разложения (1.71), например, нулевой или первой гармоникой. Если в качестве признаков селекции или распознавания образов объектов используются коэффициенты ортогонального разложения, то максимальное число тестовых сигналов определяется размерностью рабочего словаря признаков.

Рассмотрим тестовые сигналы, вид которых следует из представления пространственного спектра этого сигнала в виде дискретной выборки значений его спектральных составляющих.

Пусть сигнал от объекта, описываемый, например, в терминах спектральной яркости, ограничен в пространстве в пределах некоторой области прямоугольной формы с размерами . Будем считать, что вектор параметров априори известен. Тогда в выражении, описывающем сигнал, можно опустить зависимость от и представить этот сигнал функцией с разделяющимися переменными в виде

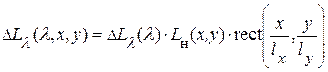, (17)

где

функция, описывающая приращение спектральной яркости относительно фона;

нормированная функция, описывающая пространственное распределение яркости излучения по поверхности объекта.

Согласно теореме Котельникова (в приложении к пространственно-частотной области) фурье-образ функции может быть представлен интерполяционным рядом вида

.

(18)

Вычислив обратное преобразование Фурье от выражения (18), получим описание сигнала в координатной области в следующем виде

(19)

Выражение (19) можно рассматривать, как разложение в ортогональном базисе, причем ортогональный базис образован функциями вида

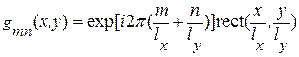.. (20)

Если воспользоваться свойством центральной симметрии двумерного фурье-спектра, то формулу (19) можно записать в виде

(21)

где спектр фаз комплексной функции .

В таком представлении базисными функциями являются ограниченные в пределах габаритных размеров действительные гармонические функции

. (22)

Из выражений (19) и (21) следует, что любой физически реализуемый сигнал, определенный в ограниченной прямоугольной области координатного пространства, может быть представлен суперпозицией ограниченных в той же области гармонических функций, имеющих пространственные частоты и . Амплитуды этих гармонических составляющих определяются значениями модуля пространственного спектра сигнала на тех же частотах, а фазы – соответствующими значениями пространственного спектра фаз.

Полученный результат является теоретическим обоснованием правомочности использования тест-объектов в виде ограниченных в координатной области гармонических решеток.

Важно отметить, что описанное выше представление тестовых сигналов может быть использовано и для моделирования случайных фоновых полей.

Дата добавления: 2014-01-06