Симплекс-метод

Каноническая форма записи задач линейного программирования

Канонической формой записи задачи линейного программирования (КЗЛП)

называют задачу вида

Z(X) = CX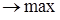

при ограничениях

AX = B, X 0

Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж. Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение). Оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций).

Переход к следующему опорному производится на основе метода Жордана-Гаусса для системы линейных уравнений. Поэтому исходная ЗЛП должна быть записана в стандартной форме.

Симплекс-метод основан на следующих свойствах ЗЛП:

1. Не существует локального экстремума, отличного от глобального. Другими словами, если максимум (или минимум) имеется, то он единственный.

2. Каждой угловой точке многогранника соответствует тот или иной опорный план.

3. Целевая функция достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Рассмотрим решение ЗЛП симплексным методом на примере ранее рассмотренной задачи (см. пример 1).

Пример 2. Минимизировать функцию

-

(36) (37)

при ограничениях

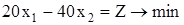
3x₁ + 4x₂ + x₃ = 1700,

2x₁ + 5x₂ + x₄ = 1600,

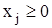, j = 1, …, 4.

Принимая в качестве базисных переменных x₃ и x₄, получаем исходный опорный план:

x₁ = 0, x₂ = 0, x₃ = 1700, x₄ = 1600.

Функция Z имеет нулевое значение, так как она выражена через небазисные переменные, которые имеют нулевые значения.

Как в таком случае можно уменьшить значение функции Поскольку x₁ и x₂ должны быть неотрицательны, любое изменение их значений приведет к убыванию функции Z, так как коэффициенты при x₁ и x₂ отрицательны.

Вместо того чтобы увеличивать их значение одновременно, для простоты выберем одну из переменных. Так как коэффициент при x₂ больше по модулю, выбираем x₂.

Однако при увеличении x₂ значения x₃ и x₄ будут изменяться, поскольку должны выполняться уравнения (36) и (37). Все переменные при этом будут неотрицательными. Таким образом, должен существовать предел увеличения x₂.

Из уравнения (36) следует, что x₃ обращается в нуль при x₂ = 1700/4 = 425.

Из уравнения (37) получаем, что x₄ обращается в нуль при x₂ = 1600/5 = 320.

Таким образом, мы не можем увеличивать x₂ более чем до 320 (минимального из этих значений), не нарушая условие неотрицательности.

Так как это значение x₂ получено по второму ограничению, то необходимо вывести из базиса содержащуюся в этом уравнении переменную х_4.

Затем необходимо исключить по методу Гаусса переменную x₂ из уравнения (36) и выражения для целевой функции.

Разделив уравнение (37) на 5 (коэффициент при x₂ в том же уравнении), запишем второе ограничение в следующем виде:

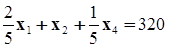. (38)

Если вычесть уравнение (38), умноженное на 4 (коэффициент при x₂ в первом ограничении), из уравнения (36), а затем вычесть уравнение (38), умноженное на -4 (коэффициент при x₂ в целевой функции), из выражения для целевой функции, то переменная x₂ будет исключена отовсюду, кроме второго ограничения, куда она входит с коэффициентом 1.

Ограничения и целевая функция принимают вид:

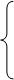
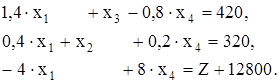(39)

Уравнения (39) являются стандартной формой для базиса x₂, x₃, представляющего базисное допустимое решение.

Небазисными стали переменные x₁ и x₄. В данный момент они равны нулю. Теперь можно уменьшить значение функции Z только за счет увеличения переменной x₁. Но насколько можно увеличить x₁, чтобы x₂ и x₃ оставались неотрицательными?

В первом уравнении x₃ обращается в нуль при x₁ =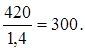

Во втором уравнении x₂ обращается в нуль при x₁ =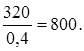

Таким образом, нельзя увеличивать x₁ более чем до 300 (минимального из этих значений).

Так как допустимое значение x₁ определено по первому ограничению, необходимо исключить эту переменную из второго ограничения и целевой функции.

После деления 1-го ограничения на 7/5 (коэффициент при x₁) получаем:

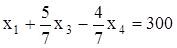. (40)

Исключим x₁ из второго уравнения системы уравнений(39), вычтя из него уравнение (40), умноженное на 2/5 (коэффициент при x₁ во втором ограничении).

Затем вычтем уравнение (40), умноженное на коэффициент -4, из целевой функции, представленной в системе уравнений (39).

В результате получим стандартную форму задачи в базисе x₁, x₂. Она имеет следующий вид:

(41)

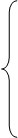
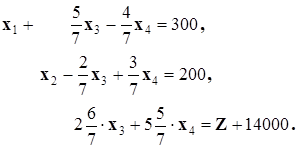
Анализируя уравнение (41), приходим к выводу, что увеличение небазисных переменных x₃ и x₄ приведет к возрастанию функции Z, так как эти переменные входят в выражение (41) с положительными коэффициентами. Следовательно, дальнейшее убывание функции Z невозможно, т. е. найдено минимальное значение целевой функции, равное - 14000 при допустимом базисном решении:

x₁ = 300, x₂ = 200, x₃ = 0, x₄ = 0.

Если вернуться к геометрической интерпретации задачи (рис.8), то можно убедиться, что последовательность стандартных форм приводит из точку 0 в точку А, а затем - из точки А в точку В – точку минимума.

Если бы на первом шаге итерационного процесса было увеличено значение x₂, то эта процедура привела бы из точки 0 в точку С, а на следующем шаге – из точки С в точку В. В результате будет получено то же решение.

Этот итерационный процесс обычно представляется в виде симплекс-таблиц (таблица 3).

В симплекс-таблице 0 звездочкой отмечено значение 5 – коэффициент при пе­ременной, которую мы собираемся обратить в базисную. В симплекс-таблице 1 точно так же отмечено число 7/5. Заметим также, что полужирным шрифтом указаны значения переменных, которые должны быть нулевыми, в отличие от переменных, обращающихся в нуль случайно.

Таблица 3.

Номер симплекс- таблицы	Базис	Значение	x1	x2	x3	x4
	x3 x4			5^*
Z		-20	-40
I	x3 x2		7/5^* 2/5			-4/5 1/5
Z	-12800	-4
II	x1 x2				5/7 -2/7	-4/7 3/7
Z	-14000			20/7	40/7

Дата добавления: 2014-01-06