
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория двойственности в линейном программировании
|
|
|
|
Открытая транспортная задача
Транспортная задача
Практически все задачи линейного программирования можно решить, используя ту или иную модификацию симплексного метода. Однако существуют более эффективные вычислительные процедуры решения некоторых задач линейного программирования, основанные на специфике решения этих задач.
Рассмотрим так называемую транспортную задачу по критерию стоимости, которую можно сформулировать следующим образом.
В m пунктах отправления А1, А2,..., Аm , которые в дальнейшем будем называть поставщиками, сосредоточено определенное количество единиц однородного продукта, под которым понимается оборудование, материалы, изделия, электроэнергия и т.п.. Количество продукта, имеющегося у каждого поставщика,
обозначается ai (i = 1, 2, …, m). Данный продукт потребляется в n пунктах В1, В2, …, Вn, которые будем называть потребителями, объем потребления каждым из них обозначается 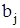 (j = 1, 2, …, n). Известны расходы на перевозку единицы продукта из пунктов Аi в пункты
(j = 1, 2, …, n). Известны расходы на перевозку единицы продукта из пунктов Аi в пункты 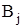 , которые равны
, которые равны 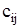 и приведены в матрице транспортных расходов C = (
и приведены в матрице транспортных расходов C = (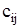 ).
).
Требуется составить такой план перевозок, при котором общая величина транспортных издержек будет минимальной.
Обозначим количество продукта, перевозимого из пункта Аi в пункт Bj через 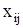 . Совокупность всех переменных
. Совокупность всех переменных 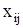 есть матрица перевозок, которую для краткости обозначим
есть матрица перевозок, которую для краткости обозначим 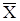 , тогда целевая функция будет иметь вид:
, тогда целевая функция будет иметь вид:
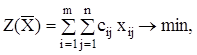 (42)
(42)
При этом ограничения выглядят следующим образом:
|
|
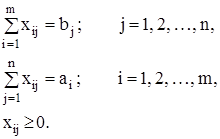
Условия (43) означают полное удовлетворение спроса во всех пунктах потребления; условия (44) определяют полный вывоз продукции от всех поставщиков.
Необходимым и достаточным условием разрешимости изложенной выше задачи является условие баланса:
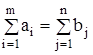 (45)
(45)
Транспортная задача, в которой имеет место равенство (45), называется закрытой и может быть решена, как задача линейного программирования с помощью симплексного метода. Однако благодаря особенностям переменных задачи и системы ограничений разработаны специальные, менее громоздкие методы ее решения.
Наиболее часто для решения транспортных задач применяется метод потенциалов, при котором каждой i-й строке (i-му поставщику) устанавливается потенциал ui, а каждому столбцу j (j-му потребителю) потенциал 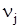 .
.
Первым этапом решения задачи по этому методу является составление начального распределения (начального плана перевозок). Для реализации этого этапа имеется в свою очередь ряд методов: северо-западного угла, наименьших стоимостей и др.
Вторым этапом является проверка оптимальности полученного плана перевозок, которая проводится с помощью метода потенциалов.
В случае неоптимальности плана переходят к третьему этапу - корректировке плана перевозок, после чего опять переходят ко второму этапу.
Совокупность процедур второго и третьего этапов составляет одну итерацию. Эти итерации повторяются до тех пор, пока план перевозок не окажется оптимальным.
Если баланс (45) не выполняется, то ограничение (43) или ограничение (44) имеют вид неравенств типа «меньше или равно». Транспортная задача в таком случае называется открытой.
Для решения открытой транспортной задачи методом потенциалов ее сводят к закрытой задаче путем ввода или фиктивного потребителя, если неравенством является ограничение (44), или фиктивного поставщика, если неравенством является ограничения (43).
Необходимо иметь в виду, что число независимых уравнений, которые могут быть составлены при решении открытой транспортной задачи, равно m + n – 1,
где m – число поставщиков, n – число потребителей.
Таким образом, из общего числа неизвестных m×n базисных неизвестных будет только m + n – 1.
Вследствие этого при любом допустимом базисном распределении в таблице перевозок будет заполнено m + n – 1 клеток (ячеек), которые будем называть базисными в отличие от остальных, свободных, клеток. Занятые клетки будем
отмечать диагональной чертой (см. пример 3).
Пример 3. Для выполнения работ в пунктах A, B, C и D требуется соответственно 18, 26, 19 и 12 автомобилей.
В гаражах Г1, Г2 и Г3имеется соответственно 20, 25 и 30 свободных автомобилей.
Расстояния от гаражей до пунктов выполнения работ приведены в таблице 4
Таблица 4
| Гаражи | Расстояния до пунктов | |||
| А | В | С | D | |
| Г1 | ||||
| Г2 | ||||
| Г3 |
Как следует распределить автомобили по пунктам выполнения работ, чтобы
минимизировать их суммарный пробег?
Так как суммарные количества потребных и свободных автомобилей совпадают, то транспортная задача является закрытой.
При решении транспортных задач удобнее не рассматривать ограничения, а
работать с массивом транспортных данных в том виде, в каком они приведены в
таблице 5.
Значения, приведенные в левых верхних углах клеток таблицы 5, соответствуют данным таблицы 4.
Таблица 5 – Начальный опорный план
| Количество автомобилей в гаражах | Количество автомобилей по объектам выполнения работ | ui | |||||||
 5 5
|
| ||||||||
 12 12
|   30 30
|
| -32 | ||||||
  35 35
|  10 10
| -30 | |||||||
| nj | -20 | -12 | -20 | 
|
Построим начальный опорный план по методу наименьших стоимостей.
Поскольку задача состоит в минимизации общего пробега, находим наименьшее расстояние 5 в строке 1, столбце 2 и присваиваем переменной x12 значение 20 (меньшая из сумм по строке и столбцу). Отмечаем заполненную клетку диагональной чертой и вычеркиваем 1-ю строку, так как все автомобили 1-го гаража задействованы.
Далее заполняется клетка (3, 4), имеющая наименьшее значение 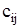 в оставшихся строках; записываем значение x34 =12 - меньшее из значений по строке и столбцу - и вычеркиваем 4-й столбец.
в оставшихся строках; записываем значение x34 =12 - меньшее из значений по строке и столбцу - и вычеркиваем 4-й столбец.
В оставшихся клетках наименьшее расстояние имеет клетка (2; 1). Присваиваем переменной x21 значение 18 и вычеркиваем 1-й столбец.
Затем переходим ко второй строке, выбираем по принципу наименьших стоимостей клетку (2;3), записываем значение x23 = 7 (так как 25 – 18 =7) и вычеркиваем вторую строку.
Оставшиеся 2 клетки 3-го столбца заполняем, руководствуясь принципом соблюдения баланса по столбцам:
x32 = 26 - 20 = 6;
x33 = 19 -7 = 12.
Таким образом, число занятых клеток равно 6.
Определим число базисных клеток:
m + n – 1= 3 + 4 – 1 = 6,
т.е. получено базисное начальное распределение.
Определим значение целевой функции:
Z(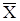 ) = 5×20 +12×18 + 20×7 + 35×6 + 18×12 +10×12 = 1002 км
) = 5×20 +12×18 + 20×7 + 35×6 + 18×12 +10×12 = 1002 км
Произведем проверку оптимальности полученного плана перевозок.
Принимаем потенциал 1- й строки u1 = 0.
Потенциалы остальных строк и столбцов определяем, используя формулу
nj = ui + cij ,
где nj потенциал j-го столбца;
cij – транспортные расходы (в данном случае пропорциональны расстоянию от i-го гаража до j-го пункта назначения; поэтому в расчетах используются
расстояния между этими объектами).
n2 = u1 + c12 = 0 + 5 = 5;
u3 = n2 - c12 = 5 – 35 = -30;
n3 = u3 + c33 = -30 + 18 =-12;
n4 = u3 + c34 = -30 + 10 = -20;
u2 = n3 - c33 = -12 - 20 = -32;
n1 = u2 + c21 = -32 + 12 = -20.
Чтобы оценить оптимальность плана перевозок, для всех клеток матрицы перевозок определяются их оценки 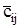 , которые вычисляются по формуле
, которые вычисляются по формуле
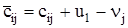 . (46)
. (46)
Очевидно, оценки занятых клеток равны нулю. Для свободных клеток отрицательное значение 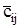 указывает на то, что переменная
указывает на то, что переменная 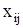 должна быть включена в базис, что приведет к уменьшению целевой функции.
должна быть включена в базис, что приведет к уменьшению целевой функции.
Оценки клеток по формуле (46) удобно представить в виде матрицы оценок:
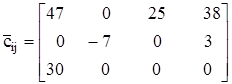 .
.
Наличие отрицательной оценки свидетельствует о том, что план неоптимален. Ясно, что увеличение x22 приведет к уменьшению целевой функции. Но насколько можно увеличить значение этой переменной, чтобы получить допустимое базисное решение?
Это можно определить следующим образом. Построим контур перераспределения, начальная вершина которого располагается в выбранной клетке, а все остальные находятся в занятых клетках. В таблице 5 этот контур показан пунктирной линией (в общем случае контур может иметь более сложную форму, линии могут пересекаться, но все углы обязательно должны быть прямыми). В вершинах контура располагаются поочередно знаки “+” и “-”, начиная со знака “+ “ в выбранной свободной клетке. Величина перераспределения определяется как наименьшая из величин 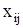 в вершинах контура, отмеченных знаком “-”.
в вершинах контура, отмеченных знаком “-”.
В данном случае это значение равно 6. Поэтому увеличим число автомобилей в клетках (2, 2) и (3, 3) на 6, и настолько же уменьшим x32 и x23.
При этом x32 становится равным нулю, т.е. клетка (3, 2) освобождается.
В результате получаем следующую транспортную таблицу.
Таблица 6 – Оптимальный план перевозок
| Количество автомобилей в гаражах | Количество автомобилей по объектам выполнения работ | ui | |||
 5 5
| -7 | ||||
  12 12
|  30 30
| -32 | |||
 35 35
|  10 10
| -30 | |||
| nj | -20 | - 2 | -12 | -20 | 
|
После корректировки плана перевозок изменятся потенциалы 2-го столбца и 1-й строки:
n2 = u2 + 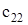 = -32 + 30 = - 2;
= -32 + 30 = - 2;
u1 = n3 - c12 = -2 -5 = -7.
Потенциалы остальных строк и столбцов не изменятся.
Определим оценки клеток улучшенного плана. Результаты расчетов представим в виде матрицы:

Так как все оценки неотрицательны, то можно утверждать, что получен оптимальный план перевозок. Кроме того, следует отметить, что в данном случае оценки всех свободных клеток больше нуля, то есть любой другой план, предусматривающий заполнение хотя бы одной из этих клеток, будет хуже найденного плана. Наличие нулевых оценок свободных клеток в оптимальном плане, наоборот, свидетельствует о том, что он не является единственно возможным.
Определим значение целевой функции для оптимального плана:
Z(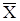 ) = 5×20 +12×18 + 20×1 + 30×6 + 18×18 + 10*12 = 960 км
) = 5×20 +12×18 + 20×1 + 30×6 + 18×18 + 10*12 = 960 км
Таким образом, в результате оптимизации плана удалось снизить суммарный пробег автомобилей на 42 км. Сравнительно небольшой эффект объясняется тем,
что начальный план перевозок составлен по наиболее эффективному методу наименьших стоимостей.
Пример 4. Рассмотрим пример открытой транспортной задачи, исходные данные которой представлены в таблице 7 (в левых верхних углах клеток этой таблицы указаны транспортные расходы 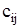 ).
).
Таблица 7 – Исходные данные открытой транспортной задачи
| Мощности поставщиков | Мощности потребителей | |||
Проверим условие баланса:
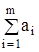 = 60 + 100 + 200 = 280;
= 60 + 100 + 200 = 280;
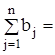 30 + 40 + 100 + 100 = 270.
30 + 40 + 100 + 100 = 270.
Условие баланса не соблюдается. Следовательно, задача действительно является открытой.
Сведем эту задачу к закрытой, введя фиктивного потребителя мощностью 280 – 70 =10. Транспортные расходы в соответствующих фиктивных клетках принимаются равными нулю, и эти клетки при составлении начального опорного плана заполняются в последнюю очередь.
Начальный план перевозок по методу наименьших стоимостей представлен в таблице 7.
Произведем проверку оптимальности полученного плана.
Принимая потенциал 1-й строки u1 = 0, определим потенциалы остальных
строк и потенциалы столбцов:
n3 = u1 + c13 = 0 + 2 = 2; n4 = u1 + c14 = 0 + 3 = 3;
u2 = n4 - c24 = 3 - 2 = 1; u3 = n4 - c34 = 3 - 4 = -1;
n1 = u2 + c21 = 1 + 1 = 2; n2 = u3 + c32 = -1 + 2 = 1;
n5 = u3 + c35 = -1 + 0 = -1.
Таблица 7 – Начальный план перевозок (начальный опорный план)
| Мощности поставщиков | Мощности потребителей | ui | ||||
 2 2
|  3 3
| |||||
 1 1
|  2 2
| |||||
 2 2
|  4 4
|  0 0
| -1 | |||
| nj | -1 | 
|
Матрица оценок клеток в соответствии с формулой (46) имеет вид:
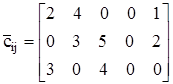 .
.
Следовательно, данный план перевозок является оптимальным и единственным. Стоимость перевозок составит 550, при этом мощности потребителей будут удовлетворены полностью, а у третьего поставщика останутся невывезенными 10 единиц груза.
Для каждой задачи линейного программирования может быть составлена другая линейная задача, называемая двойственной; первоначальная задача называется исходной, или прямой.
Связь исходной и двойственной задач заключается в том, что решение одной из них может быть получено непосредственно из решения другой.
Современные методы линейного программирования позволяют не только получать оптимальные решения с помощью эффективных вычислительных процедур, но и делать содержательные выводы, основанные на свойствах задачи, двойственной к исходной ЗЛП. Прямая задача линейного программирования записывается следующим образом:
Z(X) = 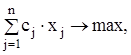 (47)
(47)
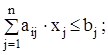 i = 1, 2, …, m; (48)
i = 1, 2, …, m; (48)
 ; j = 1, 2, …, n, (49)
; j = 1, 2, …, n, (49)
где n – число переменных 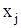 ;
;
m – число функциональных ограничений;
i –номер ограничения;
j – номер переменной.
Модель двойственной задачи имеет вид:
g(Y) = 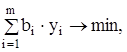 (50)
(50)
 j = 1, 2, …, n; (51)
j = 1, 2, …, n; (51)
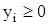 ; i = 1, 2, …, m, (52)
; i = 1, 2, …, m, (52)
где n – число функциональных ограничений;
m – число переменных yi.
j –номер ограничения;
i – номер переменной.
Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой. Однако при определении оптимального плана одной из задач находится также решение другой задачи:
max Z(X) = min g(Y).
Двойственная задача (по отношению к исходной) составляется согласно следующим правилам:
а) целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум; при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид 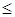 , а в задаче на минимум – вид
, а в задаче на минимум – вид  ;
;
б) матрица  ,
,
составленная из коэффициентов при неизвестных 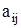 в системе ограничений (48) исходной задачи и аналогичная матрица в двойственной задаче AT получаются друг из друга транспонированием:
в системе ограничений (48) исходной задачи и аналогичная матрица в двойственной задаче AT получаются друг из друга транспонированием:
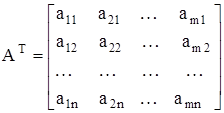 ;
;
в) число переменных в двойственной задаче равно числу функциональных ограничений (48) исходной задачи, а число ограничений (51) двойственной задачи – числу переменных исходной задачи;
г) коэффициентами при неизвестных в целевой функции (50) являются свободные члены в системе ограничений (48) исходной задачи, а правыми частями в ограничениях (51) двойственной задачи – коэффициенты при неизвестных в целевой функции (47) исходной задачи;
д) каждому ограничению одной задачи соответствует переменная другой
задачи: номер переменной совпадает с номером ограничения.
Пример 5. Модель исходной задачи имеет вид:
Z(X) = 14×x1 + 10×x2 + 14×x3 + 11×x4 ® max
4×x1 + 2×x2 + 2×x3 + 3×x4 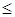 35
35
x1 + x2 + 2×x3 + 3×x4 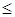 30
30
3×x1 + x2 + 2×x3 + x4 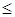 40
40
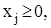 j = 1, 2, 3, 4
j = 1, 2, 3, 4
Сформулируем двойственную задачу в соответствии с приведенными выше правилами:
g(Y) = 35×y1 + 30×y2 + 40×y3 ® min
4×y1 + y2 + 3×y3  14
14
2×y1 + y2 + y3  10
10
2×y1+2×y2 +2×y3  14
14
3×y1 + 3×y2 + y3  11
11
yi  0, i = 1, 2, 3.
0, i = 1, 2, 3.
Получена симметричная пара взаимодвойственных задач. В результате решения этих задач симплексным методом найдены следующие оптимальные решения:
X = [0 5 12,5 0]; Y = [3 4 0].
Подставив полученные значения в выражения для целевых функций, получаем:
max Z(X) = 14×0 + 10×5 + 14×12,5 + 11×0 = 225
min g(Y) = 35×3 + 30×4 + 40×0 = 225
|
|
|
|
|
Дата добавления: 2014-01-06; Просмотров: 559; Нарушение авторских прав?; Мы поможем в написании вашей работы!