Критериального анализа

Исследование технико-экономической модели линии методом

Рассмотрим применение критериального анализа для решения основных технико-экономических задач на примере обобщенной модели ЛЭП. Для анализа используется следующий вариант модели для линий напряжением до 110 кВ:

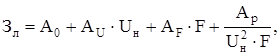
где 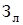– приведенные затраты;

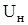– номинальное напряжение ЛЭП;

F – сечение проводов;

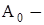постоянная составляющая затрат, не зависящая от сечения проводов и напряжения сети;

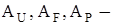обобщенные константы, характеризующие совокупность свойств исследуемой ЛЭП.

Если рассматривать только переменную часть приведенных затрат, то получаем исходное уравнение

(58)

для анализа которого используем критерии подобия.

В данной модели оптимизируемыми параметрами являются переменные затраты, номинальное напряжение сети и сечение проводов.

Выразим оптимизируемые параметры в относительных единицах:

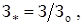
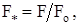
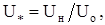
где 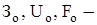оптимальные значения параметров.

Разделим обе части исходного уравнения (58) на З_* и перенесём единицу в правую часть уравнения:

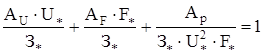
Запишем экономические критерии подобия:

В результате получаем условие нормировки критериев подобия:

Определим численные значения критериев подобия. С этой целью составим из показателей степеней оптимизируемых параметров матрицу 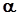, номер столбца которой соответствует номеру критерия.

	I	II	III
U*			-2
F*			-1
З*	-1	-1	-1

Найдем обратную матрицу , транспонируя которую, получим матрицу :

	I	II	III
U*	1/2	-1/4	-1/4
F*	-1/2	3/4	-1/4
З*	-1/2	-1/4	-1/4

Из матрицы найдем экономические значения критериев подобия (элементы последней строки, взятые с обратным знаком):

Следовательно, критериальное уравнение будет иметь вид:

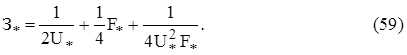
Это уравнение характеризует оптимальную структуру затрат. Значения полученных критериев подобия показывают, что в экономически целесообразном варианте ЛЭП затраты на компенсацию потерь электроэнергии равны затратам, пропорциональным сечению проводов (закон Кельвина), а их сумма составляет половину переменных затрат на линию, другая половина приходится на затраты, пропорциональные напряжению.

Одной из важнейших задач критериального анализа является исследование экономической устойчивости модели объекта. Эта задача состоит в определении степени изменения (увеличения) затрат З при отклонении оптимизируемых параметров от их оптимальных значений. Считают, что если достаточно большие изменения параметра приводят к незначительному изменению затрат, то такая модель устойчива к изменению данного параметра.

Исследование экономической устойчивости технико-экономической модели объекта заключается в определении зоны изменения параметров, в пределах которой затраты возрастают не более чем на 2 ¸ 5%.

Для исследования экономической устойчивости используются выражения

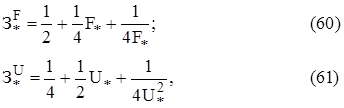
которые получены из критериального уравнения (59) при условии, что в первом уравнении U_* = 1, а во втором уравнении F_* = 1.

Результаты расчётов по уравнениям (60) и (61) позволяют сделать вывод, что исследуемая обобщённая модель ЛЭП более чувствительна к изменению напряжения, особенно в сторону его уменьшения.

Если, например, по каким-либо причинам вместо экономически оптимального сечения проводов примем в 2 раза большее или во столько же раз меньшее сечение, то относительное увеличение переменных затрат составит 12,5 %.

Если же в 2 раза завысим напряжение, то относительные затраты увеличатся на 31,3 %. В случае уменьшения напряжения в два раза относительное увеличение затрат составит уже 50 %.

Технико-экономический анализ энергетических задач обычно проводится при известных исходных данных.

Если рассматриваются задачи проектирования, исходная информация зачастую носит предположительный характер. Поэтому возникает задача исследования технико-экономической чувствительности рассматриваемой модели, то есть выяснения того, как влияет погрешность исходных данных на экономические значения оптимизируемых параметров. В практике проектирования наибольшее значение имеет чувствительность оптимальных параметров и затрат к изменению расчётной нагрузки S.

Эта зависимость имеет следующий вид

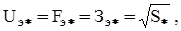(62)

где 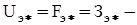экономические значения напряжения, сечения проводов и переменной составляющей приведенных затрат, о.е.;

отношение расчетной нагрузки к действительной.

Из уравнения (62) следует, что, например, при ошибочном завышении расчетной нагрузки в два раза, экономические значения параметров увеличатся на 41%.

Необходимо отметить, что исследование чувствительности проводится в относительных единицах и не требует предварительного расчета экономических значений параметров.

4 МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТАУ

Дата добавления: 2014-01-06