Математические модели отказов и восстановлений

В теории надежности обычно рассматривают объекты двух уровней сложности - элемент и система. Под элементом понимается объект, отдельные части которого не представляют существенного интереса в пределах решения рассматриваемой задачи.

Система – совокупность совместно действующих объектов, которая предна­значена для совместного выполнения определенных задач в определенных условиях.

Необходимо отметить, что элемент и система – относительные понятия. Для различных задач один и тот же объект может рассматриваться и как система, и как элемент.

Основным в теории надежностей является понятие отказа, то есть событие, заключающееся в нарушении работоспособности объекта.

Техническое устройство называется восстанавливаемым, если его работоспособность подлежит восстановлению в случае возникновения отказа, и невосстанавливаемым, если отказавшее устройство в дальнейшем не эксплуатируется.

Для того чтобы сравнивать технические устройства по надежности и оце­ни­вать эффективность разрабатываемых мероприятий, необходимо использовать количественные показатели надежности.

Рассмотрим показатели надежности, которые могут применяться в электроэнергетике.

Вероятность безотказной работы P(t) – вероятность того, что в течение времени t не произойдет ни одного отказа системы.

Вероятность отказа Q(t) – это вероятность того, что за время t произойдет хотя бы один отказ.

Вероятность отказа и вероятность безотказной работы – события несовместные и противоположные, поэтому справедливо соотношение

Q(t) = 1 – P(t)

Вероятность безотказной работы P(t) как количественная характеристика надежности обладает следующими положительными свойствами:

а) характеризует изменение надежности во времени;

б) дает возможность достаточно наглядно судить о надежности систем (элементов);

в) может быть использована для расчета надежности сложных систем.

Однако вероятность безотказной работы имеет также и существенные недостатки:

а) характеризует надежность систем только до первого отказа;

б) не всегда удобна для оценки надежности отдельных элементов системы;

в) по известной вероятности безотказной работы трудно вычислить другие количественные характеристики надежности.

Поэтому для характеристики надежности систем определяются и другие количественные характеристики.

Средняя наработка до отказа Т₁ – математическое ожидание продолжительности работы системы (элемента) до первого отказа.

Отсюда следует, что средняя наработка до отказа есть площадь, ограниченная кривой P(t) и осями координат.

Показатель Т₁ дает наглядное представление о надежности различных систем, однако он характеризует надежность системы до первого отказа, т.е является удобным для оценки надежности невосстанавливаемых систем.

Средняя наработка на отказ Т₀ определяется отношением суммарной наработки восстанавливаемых объектов к суммарному числу отказов этих объектов:

где r – число отказов системы (элемента) за время испытания t;

t_i – время работы между (i-1)-м и i-м отказами.

В отличие от средней наработки до отказа Т₁ средняя наработка на отказ Т₀ характеризует надежность восстанавливаемых объектов.

Интенсивность отказов l(t) – число отказов в единицу времени, отнесенное к числу элементов в момент времени t:

где Dn – число объектов, отказавших в интервале времени от t до t+Dt;

число объектов в момент времени t = 0;

число объектов, исправно работающих к началу рассматриваемого интервала времени.

Для систем электроснабжения функция l(t) имеет вид, изображенный на ри­сунке 27.

Как видно из графика, всю кривую можно разбить на три участка. В начальный период времени “опасность” отказа несколько повышена вследствие наличия в изделиях скрытых производственных дефектов, которые проявляются вскоре после начала работы. По мере отказа этих изделий (участок от 0 до t₁) интенсивность отказов падает. Этот период называется периодом приработки.

Второй отрезок от момента t₁ до t₂ соответствует периоду нормальной эксплу­атации изделий. Этот период характеризуется примерно постоянной интенсивностью отказов. При этом степень надежности не изменяется, так как в этот период отказы вызваны случайными причинами, не связанными со старением элемента.

Начиная с момента t₂ “опасность” отказа возрастает вследствие старения элементов системы.

Интенсивность отказов является функцией времени и позволяет наглядно установить характерные участки работы систем, что дает возможность повысить их надежность. Кроме того, зная зависимость интенсивности отказов от времени эксплуатации системы, легко определить остальные количественные показатели надежности.

Однако с помощью l(t) достаточно просто характеризовать надежность систем лишь до первого отказа.

Параметр потока отказов w характеризует надежность восстанавливаемых

систем. Он равен пределу отношения вероятности отказа системы (или элемента системы) в интервале времени от t до t + Dt к величине интервала Dt, стремящегося к нулю.

К основным показателям надежности, кроме показателей отказа, относятся также среднее время восстановления Т_в и коэффициент готовности системы К_г.

Среднее время восстановления системы электроснабжения – это среднее время вынужденного перерыва электроснабжения, вызванного отысканием и устранением одного отказа.

Среднее время восстановления системы определяется по статистическим данным:

где r– число отказов системы за определенный период эксплуатации (например, за 1 год);

t_i – время восстановления системы после i-го отказа, ч.

Коэффициент готовности – вероятность того, что система будет работоспособна в произвольно выбранный момент времени в промежутках между выполнениями планового технического обслуживания

К_г

где - время пребывания системы в работоспособном состоянии;

t_п - время вынужденного простоя вследствие отказа системы.

Помимо указанных характеристик надежности, в некоторых случаях для отражения тех или свойств конкретной электрической системы могут использоваться некоторые дополнительные характеристики. К ним относятся коэффициент отказов, коэффициент вынужденного простоя и другие.

Между количественными характеристиками надежности существует определенная взаимосвязь.

В период нормальной эксплуатации время, в течение которого элемент работает в системе, в большинстве случаев меньше времени t₂ (см. рис. 27), после которого наступает заметное старение элемента. Вследствие этого “опасность” отказов в указанный период является величиной постоянной, т.е. w(t) = const.

Поэтому наиболее употребительным законом надежности в электроэнергетике является экспоненциальный закон. Вероятность безотказной работы в этом случае имеет вид:

P(t) = .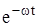

Средняя наработка на отказ при этом определяется по формуле

T₀ = .

Другой важный закон распределения, используемый в теории надежности, - это распределение Вейбулла.

Этот закон достаточно точно описывает показатели надежности элементов системы в период приработки. Период износа может быть описан как нормальным распределением, так и распределением Вейбулла.

Вероятность безотказной работы объекта при законе Вейбулла определяют по формуле

Р(t) = .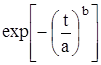

При b =1 распределение Вейбулла превращается в экспоненциальное.

Дата добавления: 2014-01-06